Julia 学习笔记(四) | 并行计算(预备篇)
Julia 笔记系列:
- 『Julia 初学者指南(一) | 安装、配置及编译器』
- 『Julia 初学者指南(二) | 数据类型与函数基础』
- 『Julia 学习笔记(二) | 类型,派发与设计模式』
- 『Julia 学习笔记(三) | 广播,性能和模块』
- 『Julia 学习笔记(四) | 并行计算(预备篇)』
- 『Julia 学习笔记(番外) | 从 Python 到 Julia』
唠唠闲话
本篇为预备内容,介绍 Julia 的并行计算,内容整理自 Julia Academic 的视频课,跳转目录:
语言交互
Julia 提供了许多语言的接口,方便语言间的交互。本节以计算求和为例,通过 Julia 提供的交互方式,比对各语言求和运算的效率。顺带介绍 Julia 中调用 C,Python 以及 Python 库的方法。
代码实验
演示使用模块 BenchmarkTools 中的宏 @btime 以及 @benchmark,代码实验在后边一节会继续介绍。
-
首次使用,需安装模块,在 Julia 中执行:
1
2using Pkg
Pkg.add("BenchmarkTools")或者用 Pkg 模式安装
1
]add BenchmarkTools
然后用
using BenchmarkTools导入模块。 -
使用
@bitme,大量重复计算右侧表达式,返回平均时间。表达式很简单时,计算次数约 ,平均时间纳秒级别,表达式越复杂,计算次数越小。 -
@benchmark统计运算信息,包括:计算次数,最小用时,最大用时,中位数用时,平均用时,以及占用内存等,比如1
2
3using BenchmarkTools
a = rand(10^7) # 随机数
sum($a) # 获取计算数据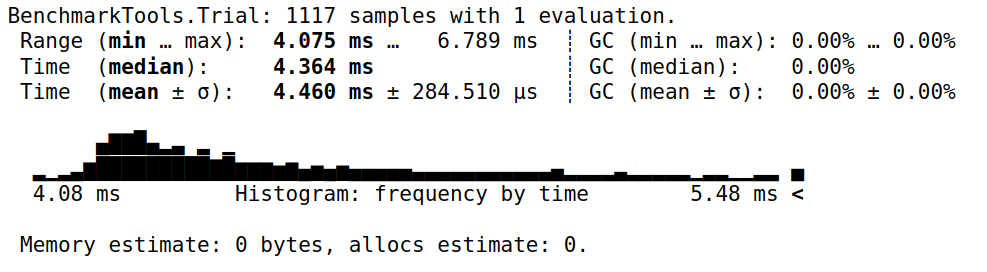
-
新建字典,记录最小用时(单位 ms),并初始化随机数据
1
2d = Dict()
a = rand(10^7);
Julia
-
内置函数最小用时
1
2
3bench = sum($a) # 获取计算数据
d["Julia"] = minimum(bench.times) / 1e6
d
-
手写函数
mysum最小用时1
2
3
4
5
6
7
8
9
10function mysum(A)
s = 0.0
for a in A
s += a
end
return s
end
j_bench_hand = mysum($a)
d["Julia hand-written"] = minimum(j_bench_hand.times) / 1e6
d
注:内置函数 sum 使用了并行计算,因而比手写版本的 mysum 更快。
C 语言
-
使用
Libdl模块,编写 C 语言代码C_code,并新建临时文件Clib1
2
3
4
5
6
7
8
9
10
11
12
13
14
15# 导入模块
using Libdl
# C 语言代码
C_code = """
#include <stddef.h>
double c_sum(size_t n, double *X) {
double s = 0.0;
for (size_t i = 0; i < n; ++i) {
s += X[i];
}
return s;
}
"""
# 临时文件
Clib = tempname() -
编译二进制文件
1
2
3
4# 编译二进制文件 .so
open(`gcc -fPIC -O3 -msse3 -xc -shared -o $(Clib * "." * Libdl.dlext) -`,"w") do f
print(f,C_code)
end -
用
ccall封装函数1
cc_sum(X::Array{Float64}) = ccall(("c_sum", Clib),Float64, (Csize_t, Ptr{Float64}),length(X), X)
-
最小用时
1
2
3c_bench = c_sum($a)
d["C"] = minimum(c_bench.times) / 1e6
d
C 语言版本和 Julia 的手写版本速度相近,但比 Julia 内置版本要慢,这是因为 Julia 内置的 sum 函数使用了并行计算。
Ps:第2步在命令行调用 gcc 的语法,第3行用 ccall 封装函数,这部分介绍再补充。
Python
-
导入模块
PyCall(需安装),使用pybuiltin封装函数1
2
3
4# 导入模块
using PyCall
# 调用 Python 内置函数
pysum = pybuiltin("sum") -
最小用时
1
2
3py_list_bench = $pysum($a)
d["Python built-in"] = minimum(py_list_bench.times) / 1e6
d
不得不说,Python 速度真拉,,,
Python 第三方库
-
安装
Conda模块,并用Conda安装Numpy1
2
3# ]add Conda # 安装 Conda
using Conda # 导入模块 Conda
Conda.add("numpy") # 安装 Numpy最后一步安装
numpy要等较长时间 -
使用
pyimport导入模块1
numpy_sum = pyimport("numpy")["sum"]
-
最小用时
1
2
3py_numpy_bench = $numpy_sum($a)
d["Python numpy"] = minimum(py_numpy_bench.times) / 1e6
d
Numpy 的 sum 和 Julia 内置的 sum 函数计算速度相近,背后也用了并行计算。
汇总比对
汇总,比对各语言计算效率
1 | for (key, value) in sort(collect(d), by=last) |

Ps:这个打印方式有点意思哈哈
初见并行
运算结合律
-
函数
mysum在执行for循环时,Julia 严格按A中元素顺序做加法1
2
3
4
5
6
7function mysum(A)
s = 0.0
for a in A
s += a
end
return s
end -
浮点数运算有精度问题,不同的加法次序带来的精度损失可能不同,因而加法不满足结合律。当使用
for循环做浮点数加法时,Julia 不希望每次运算给出不同结果,因而没有使用并行加速。1
2A = rand(10^6)
"两种求和" mysum(A) sum(A)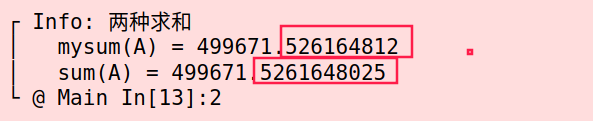
-
当精度问题无关紧要时,使用宏
@fastmath告诉 Julia 浮点运算满足结合律,此时调用for循环,Julia 便会使用并行计算加速。 -
手写函数
mysum_fast1
2
3
4
5
6
7function mysum_fast(A)
s = 0.0
for a in A
s += a
end
s
end注:宏
@fastmath将右侧运算替换为更高效的版本,此处将原先不满足结合律的浮点数求和替换为满足结合律的版本。 -
统计最小用时,与内置版本相近
1
2
3j_bench_hand_fast = mysum_fast($a)
d["Julia hand-written fast"] = minimum(j_bench_hand_fast.times) / 1e6
d
分布式
现今计算机几乎都有多个核心,上边运算在单核上进行,其他核心闲置,下边用分布式计算,进一步加快运算速度。
-
导入模块
Distributed和DistributedArrays(需安装)并添进程1
2
3
4
5# 导入模块
using Distributed
using DistributedArrays
# 添加进程
addprocs(4) -
初始化,使用宏
@everywhere1
2
3# 初始化
using DistributedArrays
workers() include("/opt/julia-1.6.3/etc/julia/startup.jl")注意
include的地址按 Julia 安装路径填写,Linux 用find命令确定路径1
2cd /
sudo find -name startup.jl -
用分布式加速内置函数
sum,速度大约快了一倍1
2
3
4
5adist = distribute(a)
j_bench_dist = sum($adist)
d = Dict()
d["Julia 4x built-in"] = minimum(j_bench_dist.times) / 1e6
d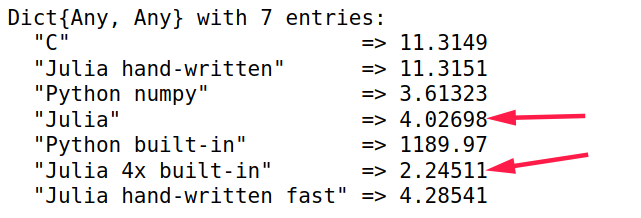
-
用分布式加速手写函数,统计最小用时
1
2
3
4
5
6
7
8
9
10
11# 手写分布式求和函数
function mysum_dist(a::DArray)
r = Array{Future}(undef, length(procs(a)))
for (i, id) in enumerate(procs(a))
r[i] = id sum(localpart(a))
end
return sum(fetch.(r))
end
j_bench_hand_dist = mysum_dist($adist)
d["Julia 4x hand-written"] = minimum(j_bench_hand_dist.times) / 1e6
d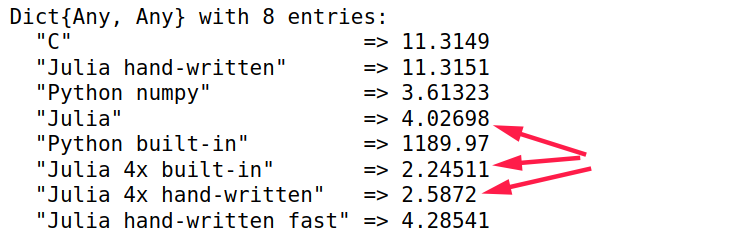
-
几种方法的最小用时排序
1
2
3for (key, value) in sort(collect(d), by=last)
println(rpad(key, 25, "."), lpad(round(value; digits=1), 6, "."))
end
Ps:分布式的语法后边细讲,这里先了解个大概。
代码实验
元编程
前边用 @bitme 和 @benchmark 做进代码实验,测试性能;又用 @fastmath 将代码替换为更高效的版本。@xxx 在 Julia 中称为 “宏”,宏背后执行的是将右侧代码当作字符或符号,生成新的代码进行替换,这种编程方式称为元编程(metaprogramming)。
常用宏
-
@show和@info用于打印信息1
21.2 typeof(1.2)
"数据及其类型" 1.2 typeof(1.2)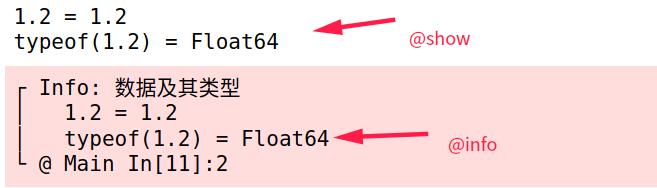
-
@assert用于声明,语法为1
@assert <expr> <description>
其中表达式
<expr>的数据类型为布尔类型,描述部分可省略,例如1
2a = -1
a > 0 "a 取值必须大于0"
-
@macroexpand查看使用宏后,实际执行的代码,比如1
a > 0 "a 取值必须大于0"

说明使用宏@assert后,代码实际执行了1
2
3
4
5if a > 0
nothing
else
Base.throw(Base.AssertionError("a 取值必须大于0"))
end -
@which查看表达式头部函数使用的方法,比如 Julia 的+函数定义了 190 种方法,使用@which查看表达式具体调用了哪个函数。1
2
3
4+
1 + 1
1.0 + 1.0
1.0 + 1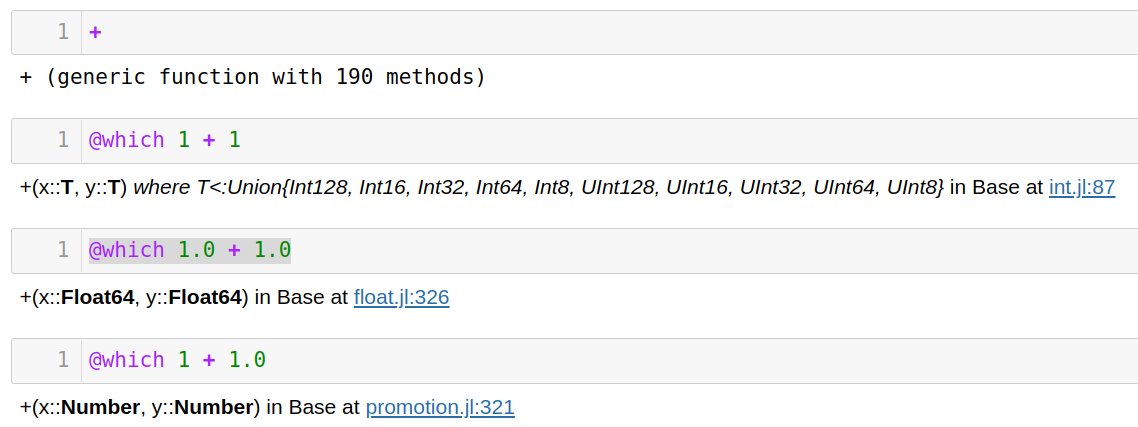
注记:
- 图中链接指向 GitHub 仓库相应的代码段
- 使用@which时,表达式并没有运行,只是检查了派发方式
- 头部函数为表达式最外层的函数,比如g(f(x))的头部函数为g -
宏可以定义自己的语法,比如
@btime的$代表引用,举几个例子- 前者每次调用,从外部获取
a,增加了内存开销
1
2
3
4
5
6using BenchmarkTools
a = rand(1000,1000)
# 方法一
sum(a)
# 方法二
sum($a)
- 前者每次调用将表达式重新计算,后者直接引用
1
2sum(a^2)
sum($(a^2))
- 一些情况下,两种方法结果可能不同
1
2
3
4
5
6# 修改变量第一个位置
function f!(a)
a[1] += 1
end
f!($[1])
f!([1])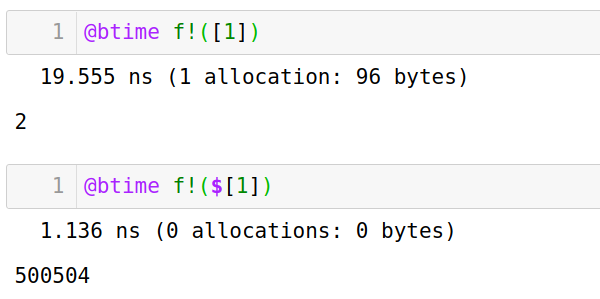
- 前者每次调用,从外部获取
代码实验
除了前边介绍了 BenchmarkTools 模块的两个宏 @benchmark 和 @btime ,还有几种宏常用语代码实验。掌握这些宏的用法读法,有助于对 Julia 类型系统的理解和使用。
-
@code_warntype查看代码中的变量类型。比如定义函数mysum时,没有声明数据类型,但实际上 Julia 在编译时自动确定了类型:1
2
3
4
5
6
7
8
9function mysum(A)
s = 0.0
for a in A
s += a
end
return s
end
a = rand(10^7)
mysum(a)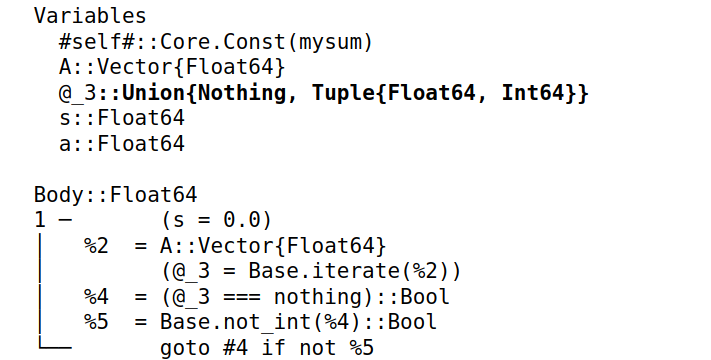
函数调用前,Julia 已经知道A为Vector{Float64}类型,s和a为Float64类型,以及输出数据(Body) 为Float64类型 -
如果类型不稳定,计算速度要慢一倍
1
2
3
4
5
6
7
8
9function mysum_unstable(A)
s = 0
for a in A
s += a
end
return s
end
mysum($a)
mysum_unstable($a)
-
@code_typed查看代码中的变量类型1
optimize=false mysum(a)

几点说明:
- 每行右侧::xxx给出变量的类型信息
- 左侧%k为第 k 行表达式值的简写
- 底部给出返回值数据类型 -
用
@code_typed查看类型不稳定时,计算过程中的变量类型1
2real_data = Real[a...]
optimize=false mysum(real_data)
类型不确定时,只能使用更低效的方法,计算速度慢 -
@profile查看计算信息1
2
3
4
5using Profile
a = rand(10^4)
Profile.clear()
for _ in 1:10000; mysum(a); end
Profile.print(maxdepth=10)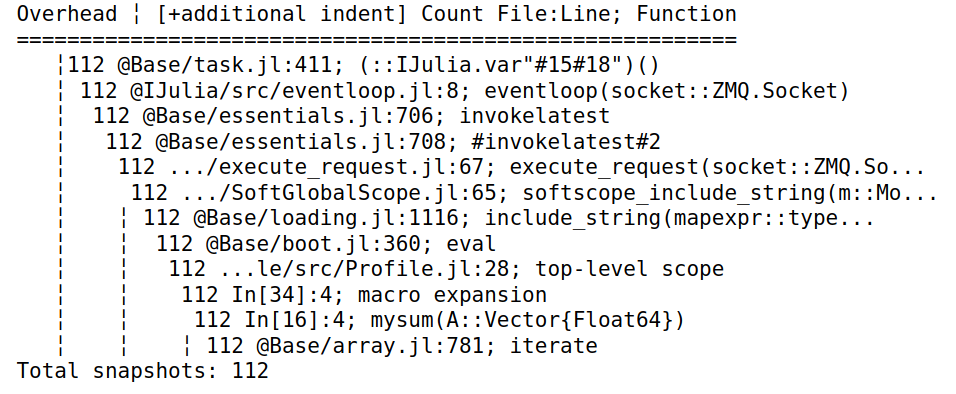
每一行中,第一个字段是在此行执行的任何函数中获取的回溯(样本)的数量。第二个字段是文件名和行号,第三个字段是函数名。缩进用于表示函数调用的嵌套序列,缩进越多的行在调用序列中越深。 -
@code_llvm理解 Julia 的运算过程以及类的确定过程(规则比较复杂,初学不深入)1
1 + .2

延伸,计算中的硬件效应:处理器与数据泄露,Microbenchmarks。
单指令多数据
单指令多数据,Single-instruction, multiple data, 简称 SIMD,有时也称为“向量化”,vectorization。简单说, SIMD 是在一核一线程上, CPU 指令集层面做的“并行”计算,这要求 CPU 支持 AVX-512,Advanced Vector Extensions 512 。
本节介绍 @simd 用法及注意事项。
例子体会
还是以求和为例,只是改用对索引进行遍历,而不是元素直接遍历。
-
使用模块,初始化数据
1
2using BenchmarkTools
A = rand(100_000) # 数字间的 _ 用于间隔排版 -
手写求和函数
1
2
3
4
5
6
7function simplesum(A)
result = zero(eltype(A))
for i in eachindex(A)
result += A[i]
end
return result
end其中
@inbounds告诉编译器索引不会溢出 -
与内置
sum比较,速度慢了 9 倍1
2simplesum($A)
sum($A)
-
改用
Float32类型,并将数据长度翻倍,数据总字节数不变1
2
3A32 = rand(Float32, length(A)*2)
simplesum($A32)
sum($A32);
-
内置函数的计算时间变动不大,而手写函数时间翻倍;原因是内置函数使用并行计算,当数据为
Float32时,数据字节减半,并行效率增倍,与长度翻倍抵消。而使用for循环遍历索引时,Julia 按顺序进行,长度翻倍则运算次数翻倍,时间相应翻倍。 -
手写函数
simdsum,并比对时间1
2
3
4
5
6
7
8
9
10
11
12function simdsum(A)
result = zero(eltype(A))
for i in eachindex(A)
result += A[i]
end
return result
end
# 比较时间
simdsum($A)
simdsum($A32)
sum($A)
sum($A32)
计算速度与内置sum相近,且处理Float64数据与处理长度翻倍的Float32数据用时相当。 -
还是前边提到的结合律问题。前边通过
@fastmath允许结合律,触发 Julia 的并行计算(向量化计算);这里则用@simd直接告诉 Julia 可以用并行处理,两种方法速度相近。1
2simdsum(A)
mysum(A)
-
对满足结合律的运算,Julia 会自动触发向量化,比如整数加法
1
2
3
4
5
6
7
8
9B = rand(1:10, 100_000)
# 不使用 @simd
simplesum($B)
# 使用 @simd
simdsum($B)
# 字节减半,长度翻倍
B32 = rand(Int32(1):Int32(10), length(B)*2)
simplesum($B32)
simdsum($B32)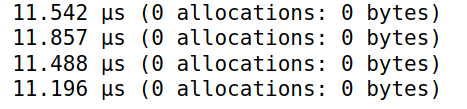
使用和不使用@simd的计算时间基本一致 -
用
@code_llvm查看是否使用了向量化1
2
3
4# for 循环做整数加法
simplesum(B)
# for 循环做浮点数加法
simplesum(A)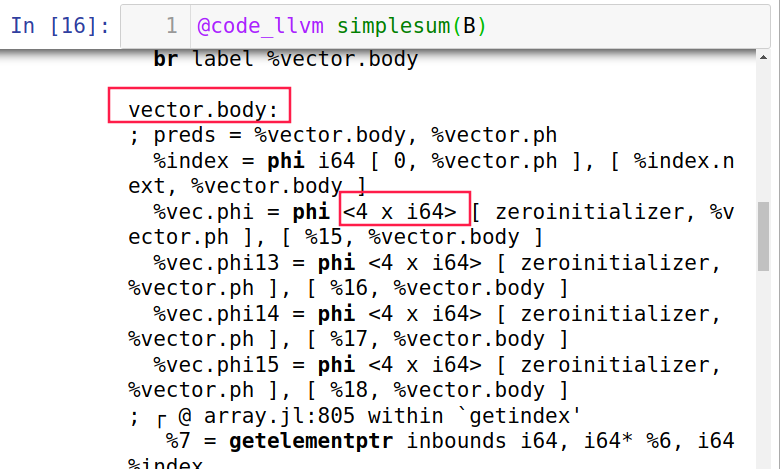
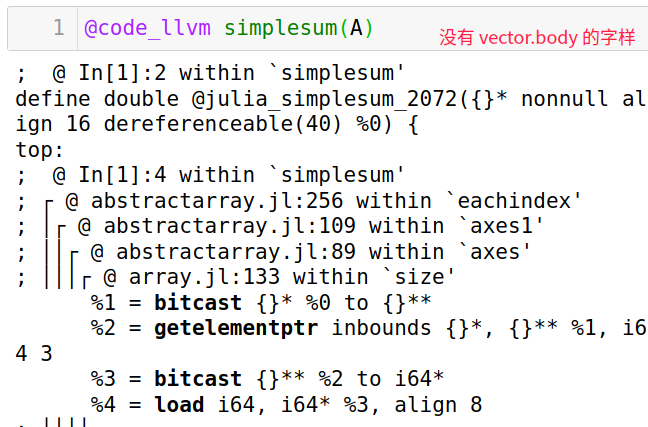
注意事项
使用 @doc @simd 查看帮助文档(谷歌翻译)
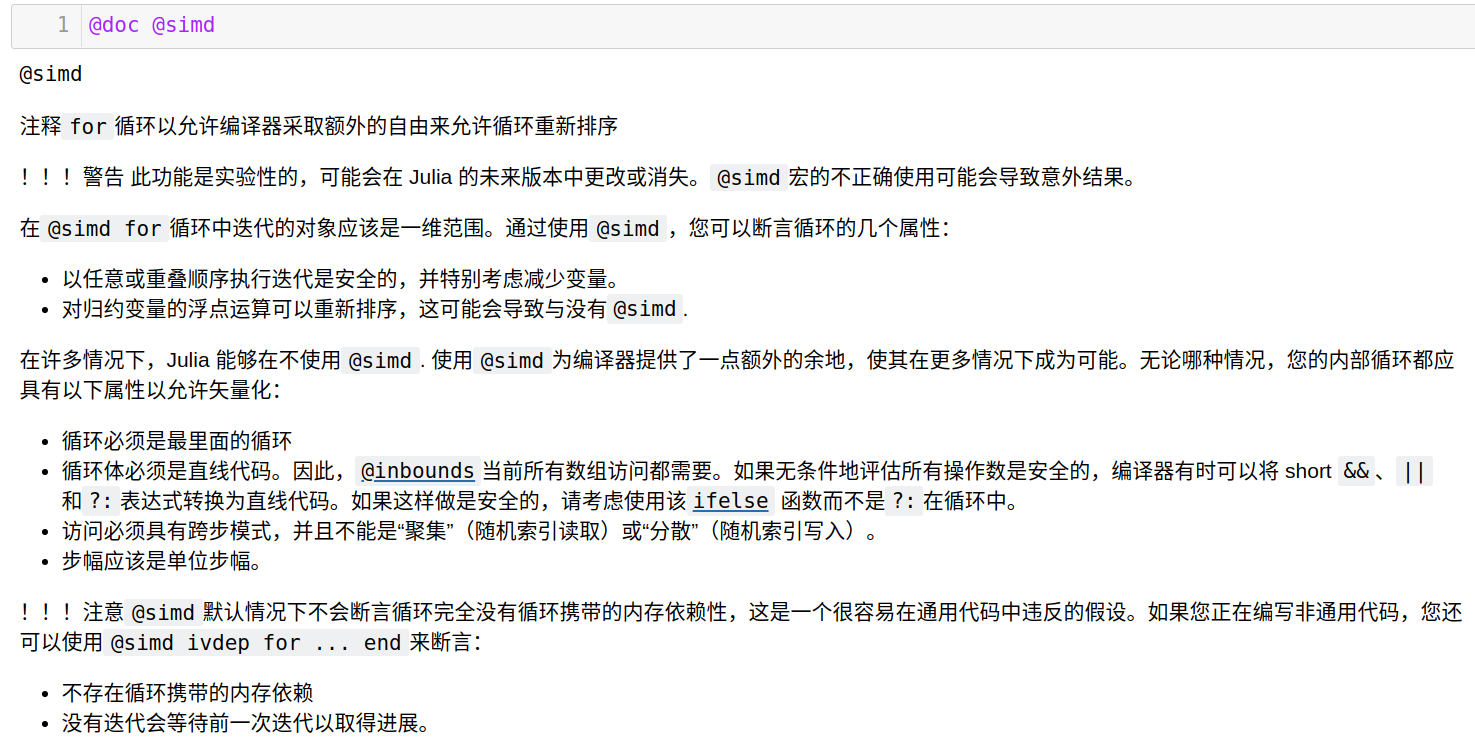
简单说,如果不正确使用 @simd 会带来一些潜在问题。举个例子:
-
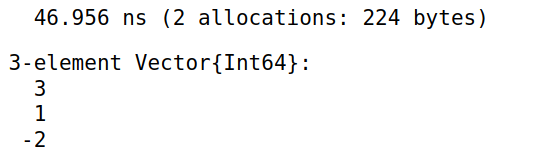
差分函数
diff用法如下,计算过程分配了内存1
diff([1,4,5,3])
-
手写函数
diff!,将差分结果放在第一个变量1
2
3
4
5
6
7
8
9
10
11
12function diff!(A, B)
A[1] = B[1]
for i in 2:length(A)
A[i] = B[i] - B[i-1]
end
return A
end
A = zeros(Float32, 100_000)
B = rand(Float32, 100_000)
diff!(A, B)
# 补上首项元素
[B[1];diff(B)] == A # true -
比较计算时间,手写版本快了一倍
1
2diff!($A, $B)
diff($B)
-
现在,将
A和B使用同一段内存,注意这样调用将导致计算结果错误1
2
3Bcopy = copy(B)
diff!($Bcopy, $Bcopy)
diff($B)
-
计算时间反而更长了,使用
@code_llvm发现,这是因为 Julia 检查到A和B使用同一内存,并行计算不安全,因而没有触发向量化1
diff!(A, B)

-
使用
@simd ivdep跳过检查,可以看到计算速度提升了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15function unsafe_diff!(A, B)
A[1] = B[1]
ivdep for i in 2:length(A)
A[i] = B[i] - B[i-1]
end
return A
end
Bcopy = copy(B)
# 内置版本
diff($B)
# 同内存版本
diff!($Bcopy,$Bcopy)
Bcopy = copy(B)
# 同内存,忽略检查版本
unsafe_diff!($Bcopy,$Bcopy)


