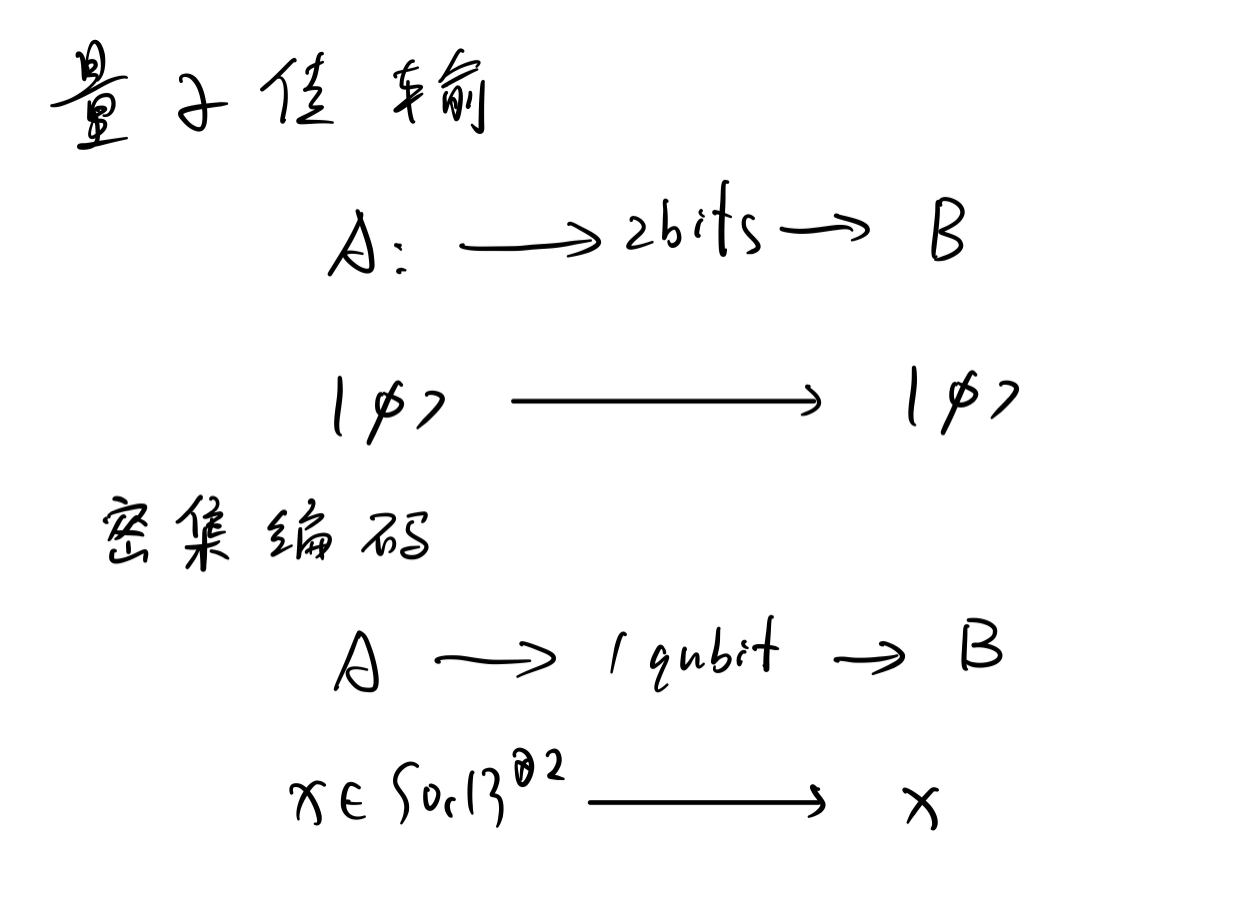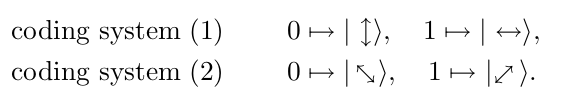量子计算系列：

唠唠闲话

量子系列第四篇，介绍量子信息传输与密钥分发技术，内容如下：

量子传输与密集编码

  1. 量子传输，Quantum Teleportation，是借助经典信道，传输未知量子比特的一种方式
  2. 密集编码，Dense coding，则是利用量子信道，传输经典比特
  3. 两种信息传输方式的形式对称，且单次传递都需要消耗一对纠缠粒子

量子传输

假设 Alice 有一个未知的量子态：

∣ϕ⟩=a∣0⟩+b∣1⟩\vert\phi\rangle=a\vert 0\rangle+b\vert 1\rangle

Alice 希望借助纠缠粒子和经典信道，将 ∣ϕ⟩\vert\phi\rangle 传递给 Bob。

从纠缠粒子分发，到量子态 ∣ϕ⟩\vert\phi\rangle 传输的量子电路图

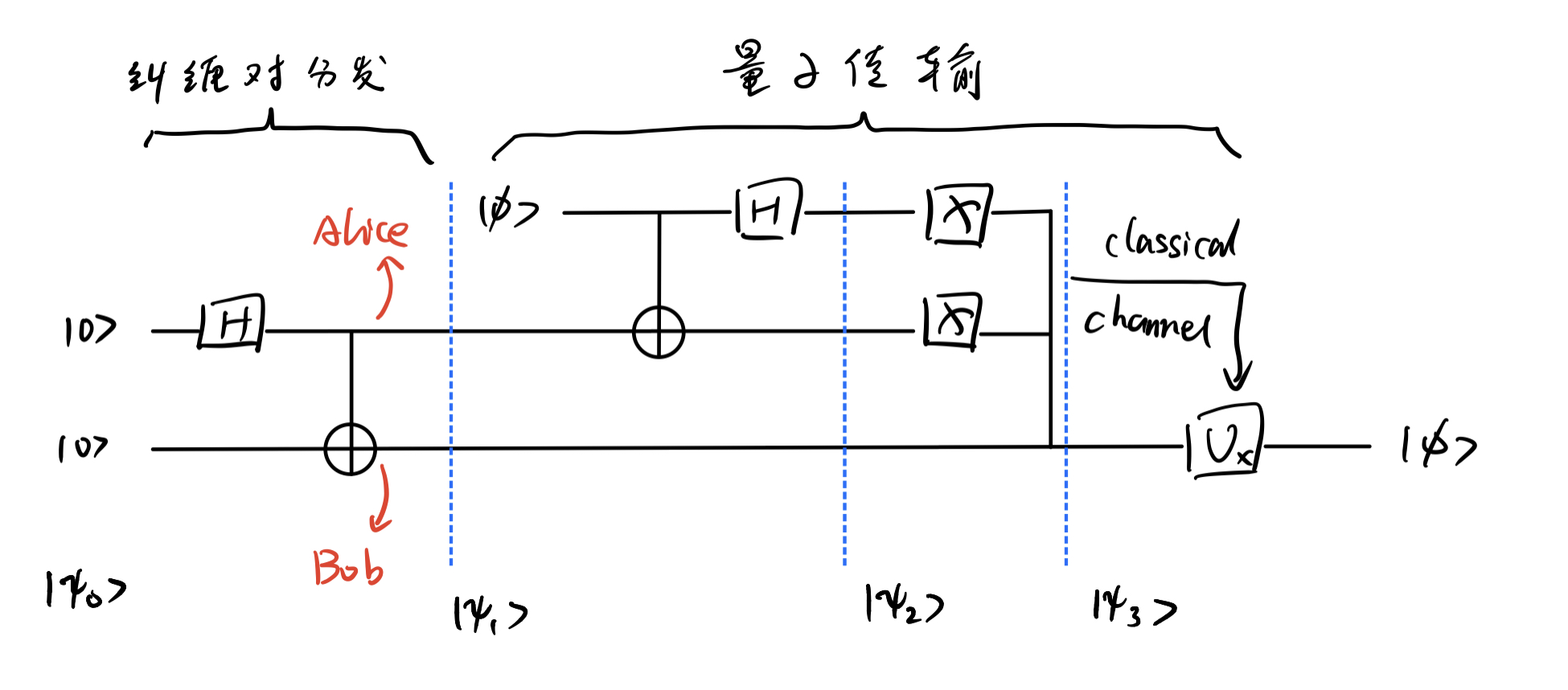
  1. 初始化量子态 ∣ψ0⟩=∣00⟩\vert\psi_0\rangle=\vert 00\rangle，通过 HH 门和受控非门转化为 Bell 态，并分发给 Alice 和 Bob。

    ∣ψ0⟩=∣0,0⟩⟶UCNOT(UH⊗I)12(∣00⟩+∣11⟩)=∣Φ+⟩\vert\psi_0\rangle=\vert 0,0\rangle\overset{U_{CNOT}(U_H\otimes I)}{\longrightarrow} \frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle)=\vert\Phi^+\rangle

  2. 现 Alice 需要传递未知量子态 ∣ϕ⟩=a∣0⟩+b∣1⟩\vert\phi\rangle=a\vert 0\rangle+b\vert 1\rangle 给 Bob；此时 ∣ϕ⟩\vert\phi\rangle 和纠缠粒子构成 3-量子系统，Alice 控制前两个，Bob 控制最后一个，系统状态为

    ∣ψ1⟩=∣ϕ⟩∣Φ+⟩\vert\psi_1\rangle=\vert\phi\rangle\vert\Phi^+\rangle

  3. Alice 通过量子门，将系统量子态变为 ∣ψ2⟩\vert\psi_2\rangle

    ∣ψ2⟩=(UH⊗I⊗I)(UCNOT⊗I)∣ψ1⟩=12(UH⊗I⊗I)(UCNOT⊗I)(a∣000⟩+b∣100⟩+a∣011⟩+b∣111⟩)=12(UH⊗I⊗I)(a∣000⟩+b∣110⟩+a∣011⟩+b∣101⟩)=12(∣00⟩⊗(a∣0⟩+b∣1⟩)+∣01⟩⊗(a∣1⟩+b∣0⟩)+∣10⟩⊗(a∣0⟩−b∣1⟩)+∣11⟩⊗(a∣1⟩−b∣0⟩))\begin{align*} \vert\psi_2\rangle &= (U_H\otimes I\otimes I)(U_{CNOT}\otimes I)\vert\psi_1\rangle\\ &= \frac{1}{\sqrt 2}(U_H\otimes I\otimes I)(U_{CNOT}\otimes I)(a\vert 000\rangle+b\vert 100\rangle+a\vert 011\rangle+b\vert 111\rangle)\\ &= \frac{1}{\sqrt 2}(U_H\otimes I\otimes I)(a\vert 000\rangle+b\vert 110\rangle+a\vert 011\rangle+b\vert 101\rangle)\\ &=\frac{1}{2}(\vert 00\rangle\otimes (a\vert 0\rangle+b\vert 1\rangle)+\vert 01\rangle\otimes (a\vert 1\rangle+b\vert 0\rangle)\\ &\quad +\vert 10\rangle\otimes (a\vert 0\rangle-b\vert 1\rangle)+\vert 11\rangle\otimes (a\vert 1\rangle-b\vert 0\rangle)) \end{align*}

  4. Alice 测量前2个粒子，依概率得到 2-bit 数据 x∈{0,1}⊗2x\in\{0,1\}^{\otimes 2} 。测量同时，Bob 粒子的量子态塌缩为 ∣ψ3⟩\vert\psi_3\rangle。

  5. Alice 通过经典信道将数据 xx 传递给 Bob，Bob 根据 xx 取值使用量子门 UxU_x，将 ∣ψ3⟩\vert\psi_3\rangle 转化为量子态 ∣ϕ⟩\vert\phi\rangle

    数据 xx 量子态 ∣ψ3⟩\vert\psi_3\rangle 量子门 UxU_x
    0000 a∣0⟩+b∣1⟩a\vert 0\rangle + b\vert 1\rangle I=∣0⟩⟨0∣+∣1⟩⟨1∣I=\vert 0\rangle\langle 0\vert+\vert 1\rangle\langle 1\vert
    0101 a∣1⟩+b∣0⟩a\vert 1\rangle + b\vert 0\rangle X=∣1⟩⟨0∣+∣0⟩⟨1∣X=\vert 1\rangle\langle 0\vert+\vert 0\rangle\langle 1\vert
    1010 a∣0⟩−b∣1⟩a\vert 0\rangle - b\vert 1\rangle Z=∣0⟩⟨0∣−∣1⟩⟨1∣Z=\vert 0\rangle\langle 0\vert-\vert 1\rangle\langle 1\vert
    1111 a∣1⟩−b∣0⟩a\vert 1\rangle - b\vert 0\rangle Y=∣0⟩⟨1∣−∣1⟩⟨0∣Y=\vert 0\rangle\langle 1\vert-\vert 1\rangle\langle 0\vert

注记：

  • Bob 得到量子态 ∣ϕ⟩\vert\phi\rangle 并不违背不可克隆定理，由于 Alice 通过测量破坏了自己的量子态
  • 数学上看，借助量子纠缠，量子态 ∣ϕ⟩\vert\phi\rangle 从第一个张量因子，移动到第三个张量因子，继而达到传送效果
  • 在 Alice 测量的瞬间，Bob 手上的量子态就塌缩了。但在不知道经典比特数据的情况下，Bob 不能得知粒子信息，因此信息传递没有超光速
  • 因为传输过程以经典数据进行，量子传输也称为量子隐形传输
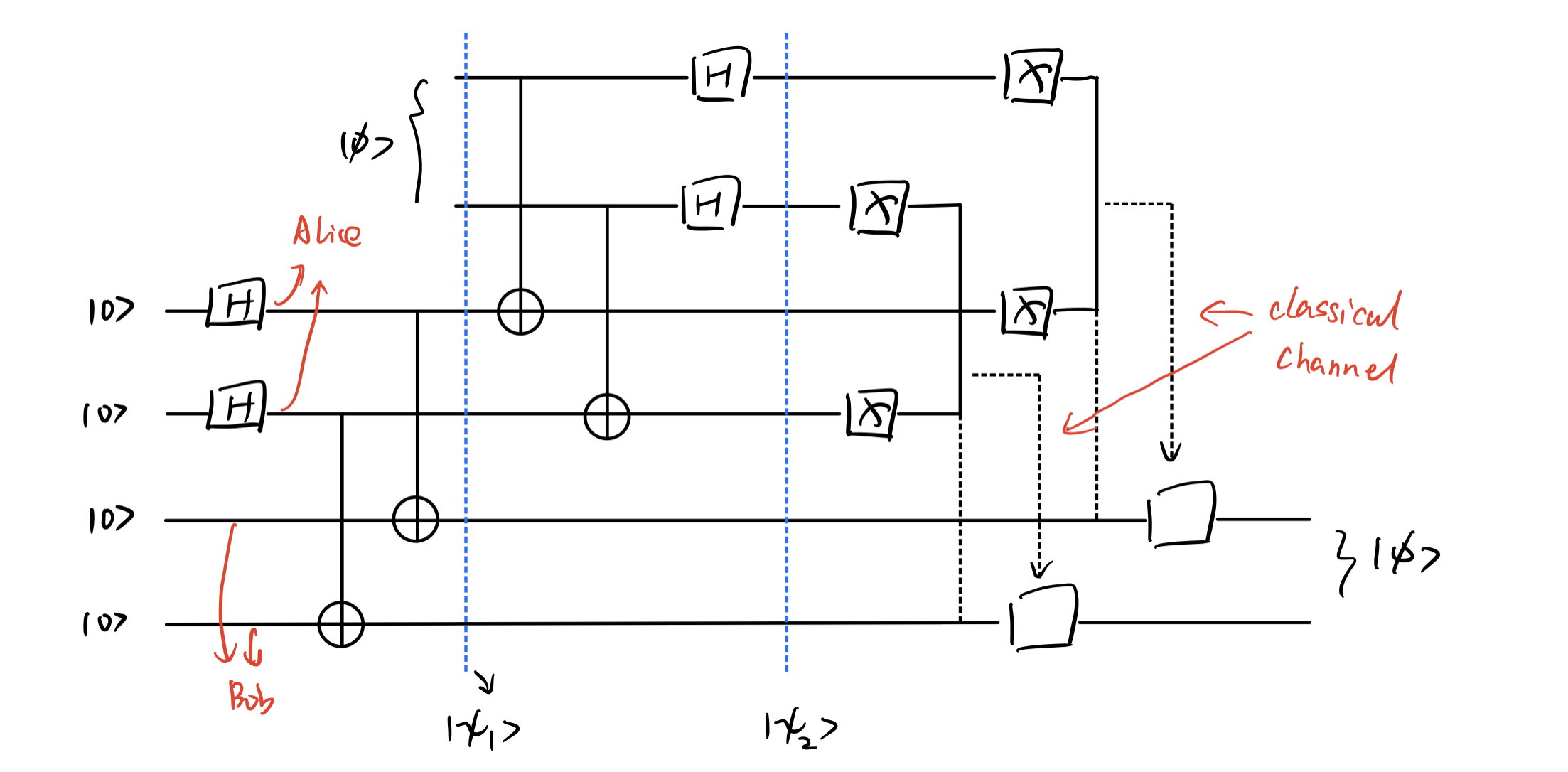
  • 纠缠粒子不能用量子传输来分发，因为传输本身就依赖纠缠粒子
  • 通过拼接，可以得到 n-粒子系统的传输，比如 n = 2 情形：
    2021-12-01_19-19-43
    一般地，Bob 根据 Alice 通过传输的 2n 比特数据 xx 选择量子门，将量子态 ∣ϕx⟩\vert\phi_x\rangle 还原为 ∣ϕ⟩\vert\phi\rangle

∣ψ1⟩=12n∣ϕ⟩(∣00⟩+∣11⟩)⊗n∣ψ2⟩=12n∑x∈{0,1}⊗2n∣x⟩∣ϕx⟩\vert\psi_1\rangle=\frac{1}{\sqrt{2^n}}\vert\phi\rangle(\vert 00\rangle+\vert 11\rangle)^{\otimes n}\\ \vert\psi_2\rangle=\frac{1}{2^n}\sum_{x\in\{0,1\}^{\otimes 2n}}\vert x\rangle\vert\phi_x\rangle

密集编码

假设 Alice 有经典数据

x∈{0,1}⊗2={00,01,10,11}x\in\{0,1\}^{\otimes 2}=\{00,01,10,11\}

Alice 希望借助纠缠粒子和量子信道，将 xx 传递 给 Bob，量子电路图：

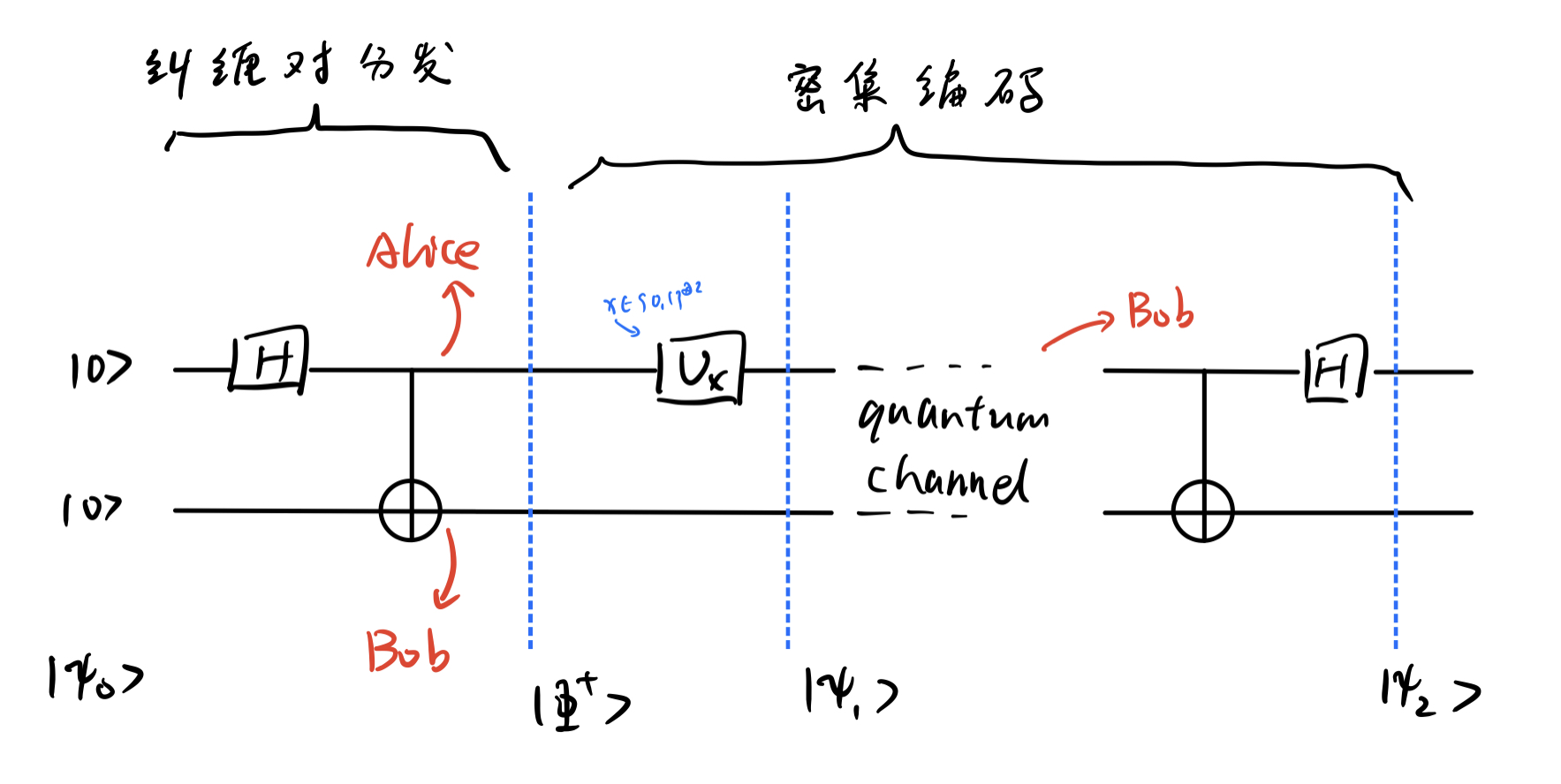
  1. 设 ∣Φ+⟩=12(∣00⟩+∣11⟩)\vert\Phi^+\rangle=\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle) 为纠缠粒子对，将第一个粒子分给 Alice，第二个粒子分给 Bob。

  2. Alice 依 xx 的取值选择量子门，作用在粒子上，系统状态变为 ∣ψ1⟩\vert\psi_1\rangle

    xx ∣Φ+⟩\vert\Phi^+\rangle UxU_x ∣ψ1⟩=(Ux⊗I)∣Φ+⟩\vert\psi_1\rangle=(U_x\otimes I)\vert\Phi^+\rangle
    0000 12(∣00⟩+∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle) I=∣0⟩⟨0∣+∣1⟩⟨1∣I=\vert 0\rangle\langle 0\vert+\vert 1\rangle\langle 1\vert 12(∣00⟩+∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle)
    0101 12(∣00⟩+∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle) X=∣1⟩⟨0∣+∣0⟩⟨1∣X=\vert 1\rangle\langle 0\vert+\vert 0\rangle\langle 1\vert 12(∣10⟩+∣01⟩)\frac{1}{\sqrt 2}(\vert 10\rangle +\vert 01\rangle)
    1010 12(∣00⟩+∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle) Z=∣0⟩⟨0∣−∣1⟩⟨1∣Z=\vert 0\rangle\langle 0\vert-\vert 1\rangle\langle 1\vert 12(∣00⟩−∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle -\vert 11\rangle)
    1111 12(∣00⟩+∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle) Y=∣0⟩⟨1∣−∣1⟩⟨0∣Y=\vert 0\rangle\langle 1\vert-\vert 1\rangle\langle 0\vert 12(∣01⟩−∣10⟩)\frac{1}{\sqrt 2}(\vert 01\rangle -\vert 10\rangle)

  3. Alice 将 ∣ψ1⟩\vert\psi_1\rangle 通过量子信道传递给 Bob。

  4. Bob 使用 UCNOTU_{CNOT} 和 UH⊗IU_H\otimes I 门作用这对粒子上：

    作用前 ∣ψ1⟩\vert\psi_1\rangle ∣ψ2⟩=UCNOT∣ψ1⟩\vert\psi_2\rangle=U_{CNOT}\vert\psi_1\rangle ∣ψ3⟩=(UH⊗I)∣ψ2⟩\vert\psi_3\rangle=(U_H\otimes I)\vert\psi_2\rangle
    12(∣00⟩+∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle) 12(∣00⟩+∣10⟩)=12(∣0⟩+∣1⟩)∣0⟩\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 10\rangle)=\frac{1}{\sqrt 2}(\vert 0\rangle+\vert 1\rangle)\vert 0\rangle ∣00⟩\vert 00\rangle
    12(∣10⟩+∣01⟩)\frac{1}{\sqrt 2}(\vert 10\rangle +\vert 01\rangle) 12(∣11⟩+∣01⟩)=12(∣0⟩+∣1⟩)∣1⟩\frac{1}{\sqrt 2}(\vert 11\rangle +\vert 01\rangle)=\frac{1}{\sqrt 2}(\vert 0\rangle+\vert 1\rangle)\vert 1\rangle ∣01⟩\vert 01\rangle
    12(∣00⟩−∣11⟩)\frac{1}{\sqrt 2}(\vert 00\rangle -\vert 11\rangle) 12(∣00⟩−∣10⟩)=12(∣0⟩−∣1⟩)∣0⟩\frac{1}{\sqrt 2}(\vert 00\rangle -\vert 10\rangle)=\frac{1}{\sqrt 2}(\vert 0\rangle-\vert 1\rangle)\vert 0\rangle ∣11⟩\vert 11\rangle
    12(∣01⟩−∣10⟩)\frac{1}{\sqrt 2}(\vert 01\rangle -\vert 10\rangle) 12(∣01⟩−∣11⟩)=12(∣0⟩−∣1⟩)∣1⟩\frac{1}{\sqrt 2}(\vert 01\rangle -\vert 11\rangle)=\frac{1}{\sqrt 2}(\vert 0\rangle-\vert 1\rangle)\vert 1\rangle ∣10⟩\vert 10\rangle

  5. 最后测量得到 xx，量子态总地变化过程：

    ∣Φ+⟩=12(∣00⟩+∣11⟩)⇒x∣ψ1⟩=(Ux⊗I)∣Φ+⟩⇒∣ψ2⟩=UCNOT∣ψ1⟩⇒∣ψ3⟩=(UH⊗I)∣ψ2⟩\begin{align*} &\vert\Phi^+\rangle=\frac{1}{\sqrt 2}(\vert 00\rangle +\vert 11\rangle)\\ \overset{x}{\Rightarrow} &\vert\psi_1\rangle=(U_x\otimes I)\vert\Phi^+\rangle\\ \Rightarrow &\vert\psi_2\rangle=U_{CNOT}\vert\psi_1\rangle\\ \Rightarrow &\vert\psi_3\rangle=(U_H\otimes I)\vert\psi_2\rangle \end{align*}

注记：

  • Alice 根据比特数据 xx 取值，选择量子门 UxU_x，将数据传入量子态，记 U=UCNOT(UH⊗I)U=U_{CNOT}(U_H\otimes I)，数学上看传递过程为共轭作用

    ∣00⟩⟶U(Ux⊗I)U−1∣x⟩\vert 00\rangle \overset{U(U_x\otimes I)U^{-1}}{\longrightarrow}\vert x\rangle

信息兑换

假设事先给 Alice 和 Bob 分发了足够的纠缠对，考虑二人之间的信息传递量：

  1. Alice 如果需要发送 2-bit 数据给 Bob，借助密度编码，只需要发送 1 qubit 数据给 Bob。
  2. Alice 如果需要发送 1-qubit 数据给 Bob，借助量子传输，只需要发送 2-bit 数据给 Bob。

这体现了信息的某种“兑换”关系，由此推导：用量子隐形传输发送 n 个量子比特，至少需要发送 2n 个经典比特数据。

反设存在某个电路图，Alice 传递 n 个未知量子比特给 Bob，只需发送 m<2nm<2n 个经典比特。现假设 Alice 需要发送 2n 个经典比特给 Bob，利用密集编码， Alice 只需发送 n 个比特给 Bob；而借助该电路图 Alice 只需发送 m<2nm<2n 个比特数据给 Bob；用 m 个比特传递 2n 个比特的信息，导出矛盾。

纠缠态与信息传输

关于纠缠态的补充。

  1. 回顾定义

    • 纠缠态：2-量子系统中，无法写成 ∣ψ⟩⊗∣φ⟩\vert\psi\rangle\otimes\vert\varphi\rangle 的纯态
    • 叠加态：纯态正交分解的一种表述
    • 混合态：测量性质只能用密度矩阵 ρ\rho 表示，无法写成向量 ∣ψ⟩\vert\psi\rangle

  2. 考虑 2-粒子系统的 Bell 态，写成纯态向量和密度矩阵形式：

    ∣Φ+⟩=12(∣00⟩+∣11⟩)ρ=∣Φ+⟩⟨Φ+∣=(1001)(1001)=(1001000000001001)\begin{align*} \vert\Phi^+\rangle&=\frac{1}{\sqrt 2}(\vert 00\rangle+\vert 11\rangle)\\ \rho&=\vert\Phi^+\rangle\langle\Phi^+\vert\\ &=\begin{pmatrix} 1 \\ 0 \\ 0 \\ 1\end{pmatrix}\begin{pmatrix} 1 & 0 & 0 & 1\end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 1 \end{pmatrix} \end{align*}

    单个粒子的测量性质由偏迹给出，局部上看，粒子处在混合态

    ρ1=tr2(ρ)=(1111)\rho_1=tr_2(\rho) =\begin{pmatrix} 1 & 1\\ 1 & 1 \end{pmatrix}

  3. 以下两种测量方式等价

    • 用可观测量 AA 测量第一个粒子 ρ1\rho_1
    • 用可观测量 A⊗IA\otimes I 测量整个系统 ∣Φ+⟩\vert\Phi^+\rangle

  4. 多量子系统中，对某个粒子使用量子门操作，不改变其他粒子的测量性质：

    Let ρ∈S(H1⊗H2)Then ρ⟶I⊗Uρ′=(I⊗U)ρ(I⊗U†)⟨A⟩=tr((A⊗I)ρ)=tr((A⊗I)(I⊗U)ρ(I⊗U†))=tr((A⊗I)ρ′)=⟨A⟩′\begin{align*} Let\ &\rho\in\mathcal{S}(\mathcal{H}_1\otimes\mathcal{H}_2)\\ Then\ \rho&\overset{I\otimes U}{\longrightarrow}\rho'=(I\otimes U)\rho(I\otimes U^\dagger)\\ \langle A\rangle &= tr((A\otimes I)\rho)\\ &= tr((A\otimes I)(I\otimes U)\rho(I\otimes U^\dagger))\\ &= tr((A\otimes I)\rho')\\ &= \langle A\rangle' \end{align*}

综上，处在纠缠态的两个粒子：

  • 对一个粒子做酉变换，不能改变另一个粒子的测量性质（否则量子态同时改变，信息传递超光速）。
  • 对一个粒子测量，另一个粒子的测量性质改变，但必须收到第一个粒子的测量数据，才能知道具体发生了什么改变。

量子密钥分发

简介

量子密钥分发，Quantum Key Distribution，简称 QKD，是一种信息物理层加密的保密通信方式，是通信过程中对携带信息的载体进行加密，这区别于传统的保密通信，后者是对信息本身进行加密传输。

以光纤中量子密钥分发和经典光纤加密通信为例。两种通信方式都是将经典 0 和 1 二进制比特信息以加密的方式传输出去，且携带 0 和 1 二进制比特信息的载体都是光脉冲，所不同的是，量子密钥分发采用的是单光子脉冲——即每脉冲包含的光子个数在单个光子水平，而经典光纤保密通信采用的是强光脉冲。此外，量子密钥分发的加密是对单光子脉冲本身进行加密，而经典光纤保密通信的加密是对传输的 0 和 1 二进制比特信息进行加密。因此，光纤中量子密钥分发可视作在通信光纤两端，利用单光子量子脉冲的发送和接收设备来替代光模块，以实现信息物理层加密的保密通信。

在量子密钥分发过程中，任何针对密钥的窃听，都需要对单光子脉冲构成的量子态进行测量，但根据量子力学不可克隆原理，任何测量都会改变量子态本身，造成高误码率，从而使窃听者被发现。

一次一密

量子密钥分发用于传递一次一密(One-Time-Pad)所需的密码本。而一次一密是不可破解的加密算法，其加密条件为：

  • 密钥和要加密的消息同样长
  • 密钥由真正随机符号组成
  • 密钥只用一次，永不对其他消息复用

不可破解原因

如果密钥和消息一样长，那么每个可能的密文字母都有相同的概率解密成相同的明文字母，这样就无法使用频率分析来工作。
举个例子，用轮盘加密，取随机密钥 10251，加密单词 apple，得到密文 bprqf：

a→+1b, p→+0p, p→+2r, l→+5q, e→+1fa \overset{+1}{\rightarrow}b,\ p \overset{+0}{\rightarrow}p,\ p \overset{+2}{\rightarrow}r,\ l \overset{+5}{\rightarrow}q,\ e \overset{+1}{\rightarrow}f

密钥未知时，任意五个字母的单词都可能由密文 bprqf 解出。

交换密码本

假设 Alice 要传送信息给 Bob，使用一次一密的最大困难在于：Alice 需事先和 Bob 交换密码本。如果在不安全信道上传输密钥原文，密钥被窃取，后续加密也就没有意义了。

之前介绍过基于数论难题，生成密码本的两种方法：

  • Diffie–Hellman 密钥交换（离散对数算法）
  • 椭圆曲线算法

而量子密钥分发是基于量子力学原理，对信息本身加密，生成密码本。

BB84协议

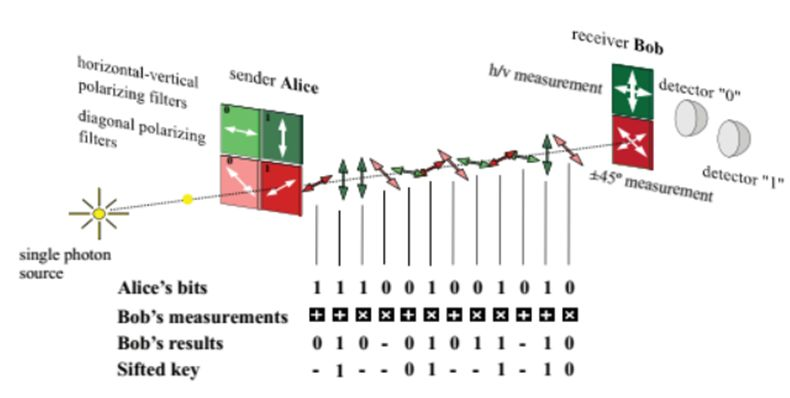
量子密钥分发的第一个协议——BB84协议是美国物理学家 Charles H. Bennett 和加拿大密码学家 Gilles Brassard 在1984年提出的，BB84 得名于两人姓的首字母和提出年份。BB84 协议属于两点式通信架构，即一个发送端（Alice），一个测量端（Bob），如下图所示：

20211123070244

加密系统

Alice 和 Bob 约定两组加密系统，比如
深度截图_选择区域_20211124092646

该加密系统有以下性质：

  • 加密系统 (1) 将比特 0 转化为量子态 ∣↕⟩\vert\updownarrow\rangle， 将比特 1 转化为量子态 ∣↔⟩\vert\leftrightarrow\rangle
  • 使用系统 (1) 测量 ∣↕⟩(∣↔⟩)\vert\updownarrow\rangle(\vert\leftrightarrow\rangle)，有 100%100\% 概率得到 0 (1)
  • 使用系统 (2) 测量 ∣↕⟩\vert\updownarrow\rangle 和 ∣↔⟩\vert\leftrightarrow\rangle，都是 50%50\% 概率得到 0， 50%50\% 概率得到 1
  • 两系统反过来的讨论结果类似

注：使用系统 (2) 测量 ∣↕⟩\vert\updownarrow\rangle，写成叠加态形式

∣↕⟩=12(∣↖⟩+∣↗⟩)\vert\updownarrow\rangle=\frac{1}{\sqrt 2}(\vert\nwarrow\rangle+\vert\nearrow\rangle)

故测得 ∣↖⟩\vert\nwarrow\rangle 和 ∣↗⟩\vert\nearrow\rangle 的概率均为 50%50\%

分发过程

假设 Alice 和 Bob 需要一段长为 NN bit 的随机密钥。

  1. Alice 生成 4N4N bit 随机数据 ε⃗\vec\varepsilon

    ε⃗=(ε1,⋯ ,ε4N), εi∈{0,1}\vec\varepsilon=(\varepsilon_1,\cdots,\varepsilon_{4N}),\ \varepsilon_i\in\{0,1\}

    然后随机选择 4N4N 个加密方式 (1) 和 (2)

    a⃗=(a1,⋯ ,a4N), ai∈{(1),(2)}\vec a=(a_1,\cdots,a_{4N}),\ a_i\in\{(1),(2)\}

    通过加密系统 a⃗\vec a，将经典数据转 ε⃗\vec\varepsilon 转为量子比特数据 ∣ψ⟩⃗\vec{\vert\psi\rangle} ，并发送给 Bob

    ∣ψ⟩⃗=(∣ψ1⟩,⋯ ,∣ψ4N⟩)\vec{\vert\psi\rangle}=(\vert\psi_1\rangle,\cdots,\vert\psi_{4N}\rangle)

  2. Bob 收到信息 ∣ψ⟩⃗\vec{\vert\psi\rangle} 后，随机选择 4N4N 个测量方式 (1) 和 (2)

    b⃗=(b1,⋯ ,b4N), bi∈{(1),(2)}\vec b=(b_1,\cdots,b_{4N}),\ b_i\in\{(1),(2)\}

    通过测量系统 b⃗\vec b，将量子数据 ∣ψ⟩⃗\vec{\vert\psi\rangle} 转为 4N4N 个经典比特数据

    δ⃗=(δ1,⋯ ,δ4N), δi∈{0,1}\vec\delta=(\delta_1,\cdots,\delta_{4N}),\ \delta_i\in\{0,1\}

  3. Alice 和 Bob 在公共信道（可能不安全）交换各自的加密系统 a⃗\vec a 和 b⃗\vec b，如果过程完全随机，a⃗\vec a 和 b⃗\vec b 约有 2N2N 个位置相同（余下 2N2N 个丢弃），设相同位置为

    t⃗=(t1,⋯ ,t2N), ati=bti\vec t=(t_1,\cdots,t_{2N}),\ a_{t_i}=b_{t_i}

    如果数据没被窃听，位置 t⃗i\vec t_i 上 Bob 和 Alice 共享了相同的比特数据

    εti=δti,∀ i=1,⋯ ,2N\varepsilon_{t_i} = \delta_{t_i},\forall\ i=1,\cdots,2N

  4. Alice 和 Bob 从这 2N2N 个结果中取出 NN 个，在公开信道上比对。如果信息错误率远低于 25%25\%，进行数据后处理，两人共享一段相同的安全密钥；否则认为此次通信不安全，放弃该次通信产生的密钥，进行下一次通信。

窃听者

假设信息 ∣ψ⟩⃗\vec{\vert\psi\rangle} 在传递过程中，被 Eve 拦截窃听。以单个量子比特 ∣ψi⟩\vert\psi_i\rangle 传递为例，分析 Alice 和 Bob 比对 NN 个比特数据时得到的错误率。不妨设 Alice 和 Bob 对 ∣ψi⟩\vert\psi_i\rangle 使用相同系统，否则 ∣ψi⟩\vert\psi_i\rangle 最终被丢弃，不在比对数据中 。

  1. Eve 拦截 ∣ψi⟩\vert\psi_i\rangle 后如下处理（错误率最低）：随机选择系统 ei∈{(1),(2)}e_i\in\{(1),(2)\}，用系统 eie_i 测量 ∣ψi⟩\vert\psi_i\rangle 得到数据 ηi\eta_i 后，继续用系统 eie_i 将 ηi\eta_i 转为量子比特 ∣ψi′⟩\vert\psi_i'\rangle，并传递给 Bob。
  2. 假设过程完全随机，Eve 有 50%50\% 的概率选择了系统 (1)，此时

    ∣ψi′⟩=∣ψi⟩\vert\psi_i'\rangle=\vert\psi_i\rangle

    Bob 测量结果正确。
  3. Eve 有 50%50\% 的概率选择了系统 (2)，此时 ∣ψi⟩\vert\psi_i\rangle 的测量结果随机；量子比特 ∣ψi′⟩\vert\psi_i'\rangle 传递给 Bob 后，Bob 的测量结果也随机。因此 Bob 有 50%50\% 的概率测量正确。
  4. 综上，Bob 的测量结果 25%25\% 的错误率。