量子计算系列:
唠唠闲话
量子系列第三篇,介绍量子门与量子电路的基础知识,内容如下
单量子门与多量子门
实现方式
数据和运算是计算机的两个重要部分。
- 经典计算:数据单位为比特,取值0或1,由二极管的通电断电实现。
- 量子计算:数据单位为量子比特,取值为 Bloch 球面向量,无穷集;由偏振光子,自旋 21 粒子等实现。
- 经典计算:运算用逻辑门,通过电路实现。
- 量子计算:运算用量子门,通过磁场等方式实现。
注记:
- 量子门对应薛定谔方程的时间演化算子,是一个酉变换,但在量子电路中简化为常量矩阵,为理想模型。
- 经典电路是现实意义的电路,电路图和实际连线方式有联系,运算在空间上连接
- 量子电路只是运算过程的抽象,电路图与物理实现方式无关,运算在时间上连接
常见逻辑门有:与,或,非,与非,或非,异或,同或,电路符号如下
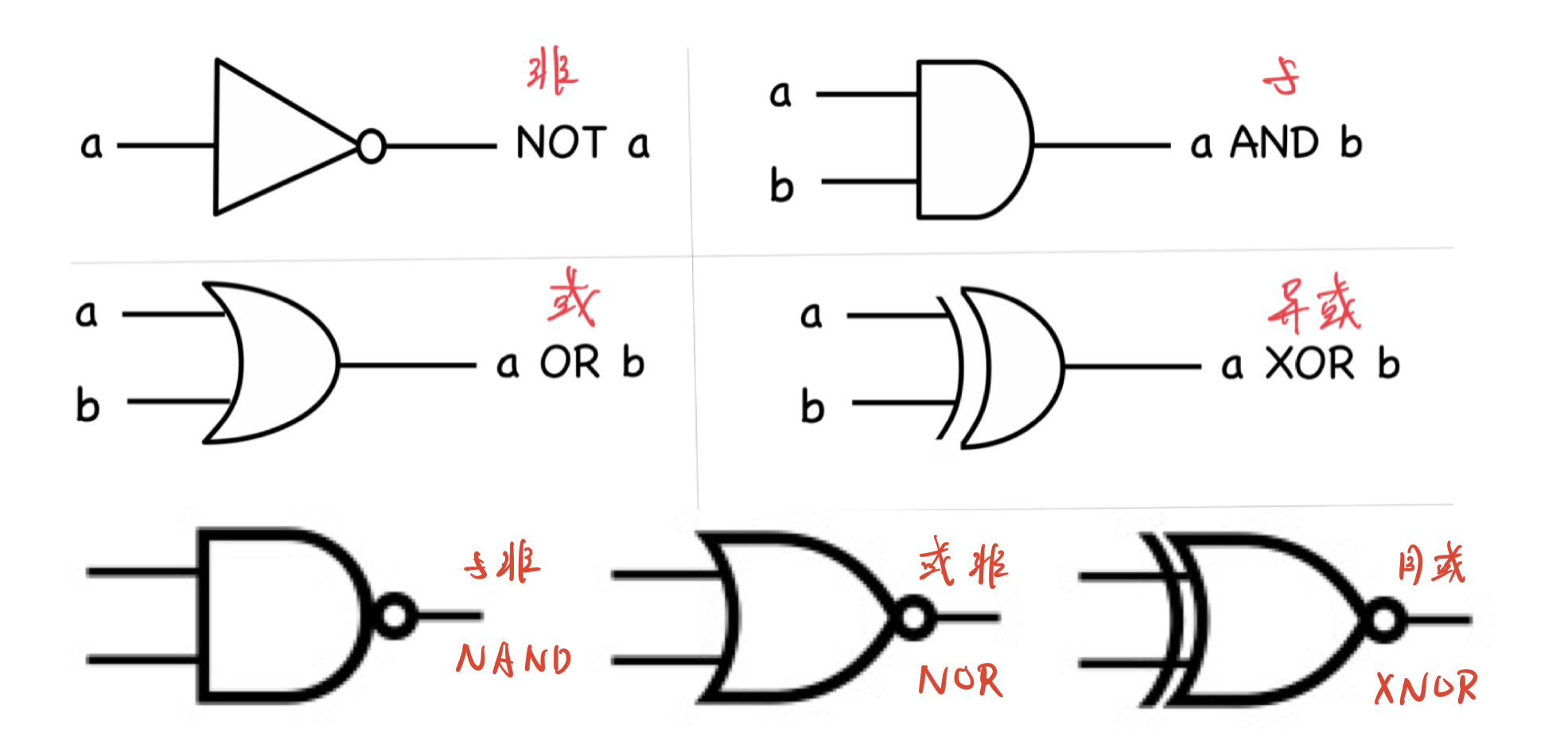
应用例子:通过“与门”和“异或门”,实现二进制数的一位数加法
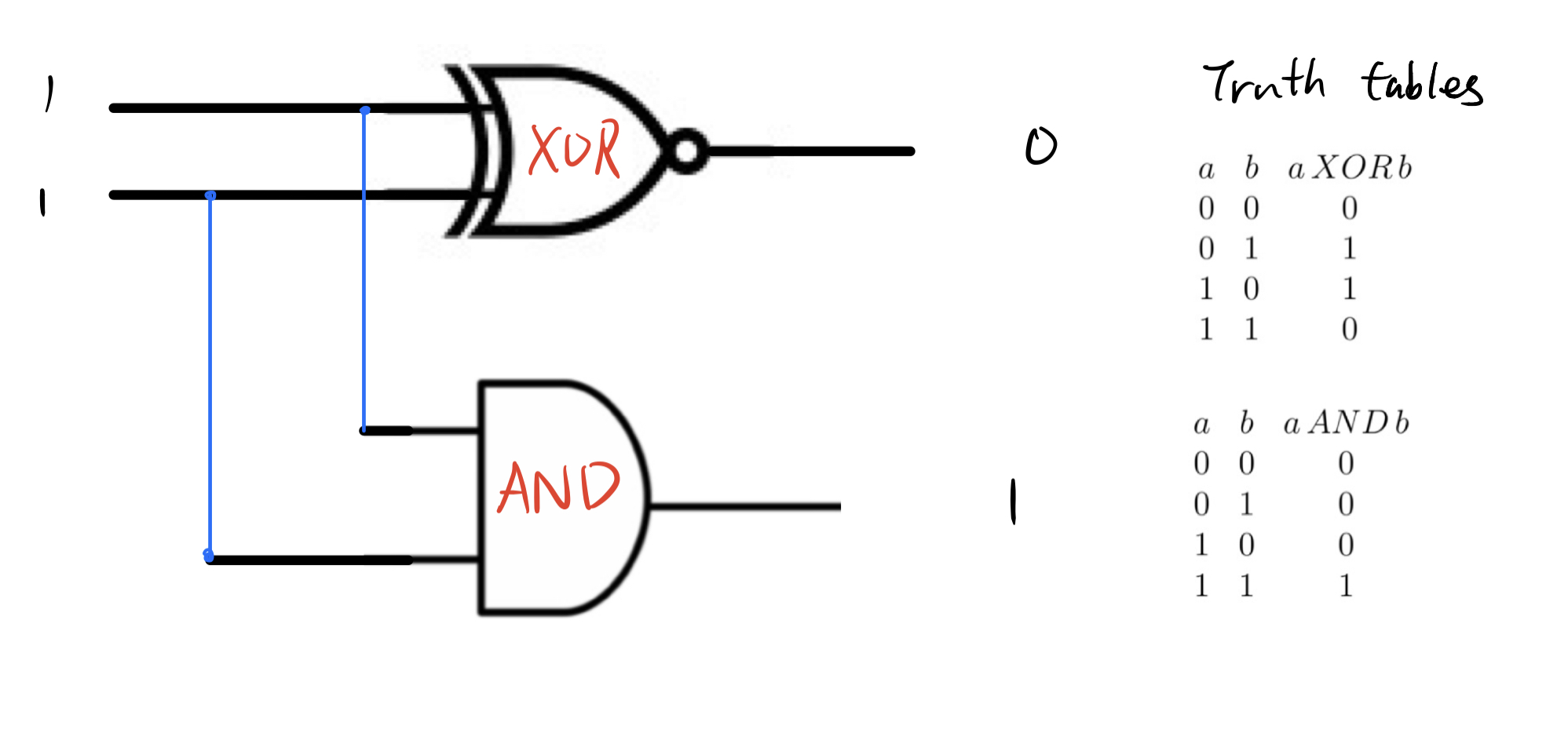
延伸:计算机是如何运算的,用加法机介绍计算机的基本组成部件。
单量子门
n 量子比特的量子门为 2n 阶酉矩阵,特别地,单量子门为 2 阶矩阵。常用的单量子门:
| 名称 |
符号 |
矩阵 |
狄拉克符号 |
| I 门 |
I |
(1001) |
∣0⟩⟨0∣+∣1⟩⟨1∣ |
| X 门 |
X, ⨁ |
σx, (0110) |
∣1⟩⟨0∣+∣0⟩⟨1∣ |
| Y 门 |
Y |
iσy, (0−110) |
∣0⟩⟨1∣−∣1⟩⟨0∣ |
| Z 门 |
Z |
σz, (100−1) |
∣0⟩⟨0∣−∣1⟩⟨1∣ |
| Hadamard 门 |
H |
21(111−1) |
21(∣0⟩+∣1⟩)⟨0∣ + 21(∣0⟩−∣1⟩)⟨1∣ |
注记:
- Y 门可以用 X 门和 Z 门生成(Y=ZX)
- X 门也称为反门,非门(negation)
- 狄拉克符号读法:∣像⟩⟨原像∣,比如 H 门的 (∣0⟩+∣1⟩)⟨0∣ 表示作用在 ∣0⟩ 上,得到纠缠态 (∣0⟩+∣1⟩)
二进制索引
-
矩阵索引从0记起,此时 ∣i⟩⟨j∣=ei,j ,比如
∣0⟩⟨1∣=(10)(01)=(0010)=e0,1
-
多量子比特系统中,将 01 序列写为二进制数
∣m⟩==where m=∣i1⋯in⟩(0 0⋯ 0 1(m) 0⋯0)t2n−1i1+⋯+2in−1+in, ik∈{0,1}
-
写法与克罗克积的定义相容,比如
∣2⟩:==∣10⟩=∣1⟩⊗∣0⟩(01)⊗(10)=⎝⎛0010⎠⎞
-
多量子门酉矩阵的第 m 行描述对量子态 ∣i1⋯in⟩ 的作用结果,比如 Toffoli 门
⎝⎛1000000001000000001000000001000000001000000001000000000100000010⎠⎞
左乘效果为最后两行置换,对应 ∣6⟩=∣110⟩ 与 ∣7⟩=∣111⟩ 的置换。
多量子门
受控门
-
受控非门,亦称为 CNOT 门,CX 门,记号 UCNOT,矩阵形式:
⎝⎛1000010000010010⎠⎞
狄拉克记号:
∣0⟩⟨0∣⊗I+∣1⟩⟨1∣⊗X
UCNOT 中,第 1 个比特称为控制比特,保持不变;第 2 个比特称为目标比特,受第 1 个比特控制。电路图:
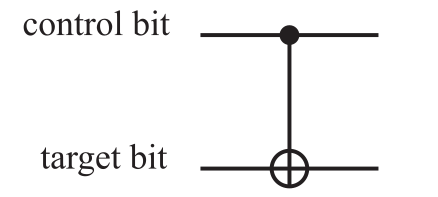
-
一般受控门的矩阵形式:
⎝⎛10001000U⎠⎞
狄拉克记号:
∣0⟩⟨0∣⊗I+∣1⟩⟨1∣⊗U
电路图:
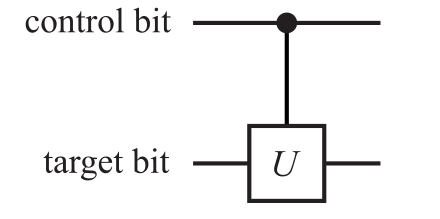
n 个比特的量子门为 2n 阶矩阵,阶数随 n 指数增长;在表现量子门作用效果时,矩阵形式不方便。使用狄拉克符号,量子门有这几种常用写法:
∣ψ1⟩⟨ψ2∣⊗∣φ1⟩⟨φ2∣=∣ψ1φ1⟩⟨ψ2φ2∣
∣i,j⟩⟶UCNOT∣i,i⊕j⟩
其中 ⊕ 为 Z2 上的加法。
∣i⟩⟶H21(∣0⟩+(−1)i∣1⟩)=210≤i<2∑(−1)i∣i⟩
通用量子门
- 单量子门与受控非门构成通用量子门,即通过二者的复合与张量,可以构造任意量子门。数学表述:
∀ U∈U(C2n), ∃ {Ui,j}⊆Universal Gates, s.t.U=(U1,1⊗⋯⊗U1,k1)⋯(Um,1⊗⋯⊗Um,km)
证明繁琐,只需知晓:实现一般量子门的关键是控制非门和任意单量子门
- 举个例子,用控制非门和 H 门,实现“颠倒”的控制非门:
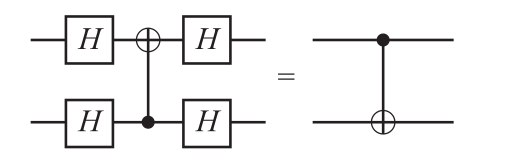
其他量子门
这几个量子门经常会用到:
-
Walsh-Hadamard 门,记号 Wn,狄拉克符号:
Wn=(UH)⊗n
特别地,W1=UH 为 Hadamard 门。
映射形式:
∣α⟩=∣i1⋯in⟩↦k=1⨂n(∣0⟩+(−1)ik∣1⟩)=2n1β∈{0,1}⊗n∑(−1)α⋅β∣β⟩
其中 α⋅β 为向量点积。
特别地,Wn 门作用量子态 ∣0⟩⊗n 上,得到 2n 种状态的叠加
0≤i<2n∑2n1∣i⟩
注:Detusch Josza 算法就是借助 Wn 门产生叠加态,做并行计算
-
UH 和 UCNOT 组合,用于构造 Bell 态,产生纠缠粒子:
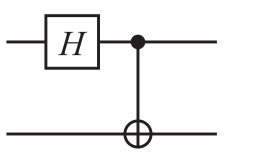
∣00⟩⟶H⊗I∣01⟩⟶H⊗I∣10⟩⟶H⊗I∣11⟩⟶H⊗I21(∣00⟩+∣10⟩)⟶UCNOT21(∣00⟩+∣11⟩)21(∣01⟩+∣11⟩)⟶UCNOT21(∣01⟩+∣10⟩)21(∣00⟩−∣10⟩)⟶UCNOT21(∣00⟩−∣11⟩)21(∣01⟩−∣11⟩)⟶UCNOT21(∣01⟩−∣10⟩)
-
交换门,记号 USWAP,用于交换比特状态:
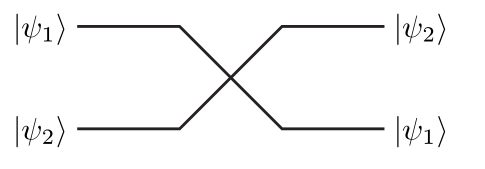
电路图写成通用量子门形式:
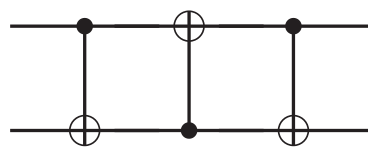
∣i,j⟩⟶UCNOT⟶UCNOT′⟶UCNOT∣i,i⊕j⟩∣i⊕(i⊕j),i⊕j⟩=∣j,i⊕j⟩∣i,(i⊕j)⊕j⟩=∣j,i⟩
-
Toffoli 门,也称为 CCNOT 门,当两个控制比特取 ∣1⟩ 时,目标比特取反。Toffoli 门可用于构造经典电路,狄拉克符号:
UCCNOT=∣0⟩⟨0∣⊗I⊗I+∣1⟩⟨1∣⊗UCNOT=(∣00⟩⟨00∣+∣01⟩⟨01∣+∣10⟩⟨10∣)⊗I+∣11⟩⟨11∣⊗X
由狄拉克符号,容易读取作用性质,两个等式对应两种视角
映射形式:
∣i0,i1,i2⟩⟶UCCNOT∣i0,i1,i0i1⊕i2⟩
矩阵形式:
⎝⎛1000000001000000001000000001000000001000000001000000000100000010⎠⎞
矩阵只有后两列“非平凡”,表明 UCCNOT 交换量子态 ∣110⟩,∣111⟩,其他不变。
电路图:
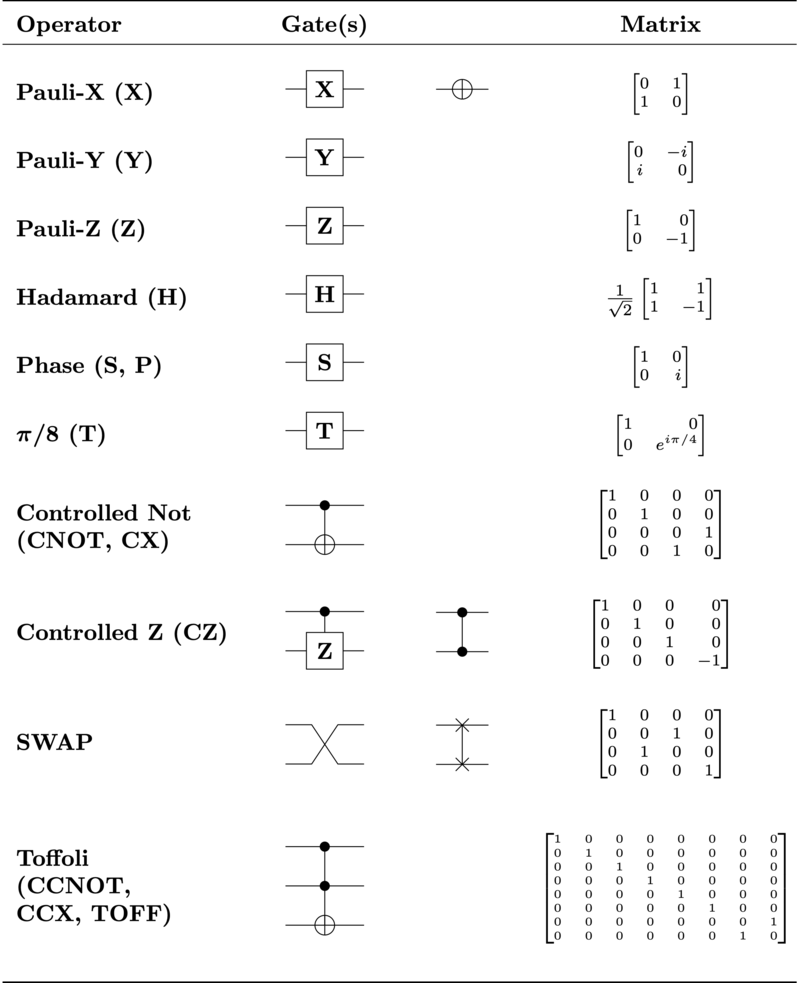
量子门记号和矩阵(wiki 百科):
Toffoli 门与逻辑门
令量子电路中的状态 ∣0⟩ 和 ∣1⟩ 与经典电路的0-1 对应。用 Toffoli 门和 X 门可以生成基本逻辑门的“与”,“或”和“非”,继而构造所有经典逻辑门。
-
“非” 运算符为 ¬,用 Toffoli 门实现:
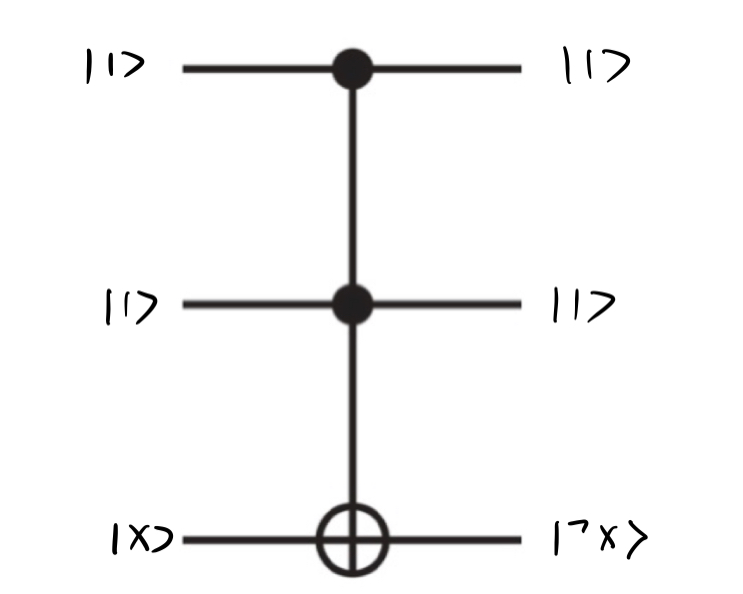
量子态变化过程:
∣1,1,x⟩⟶UCCNOT∣1,1,1⊕x⟩=∣1,1,¬x⟩
-
“与” 运算符为 ∧ ,真值表:
用 Toffoli 门实现:
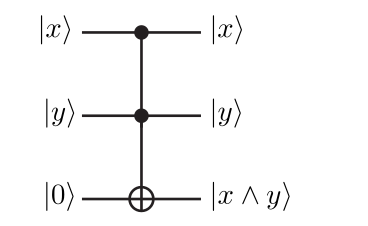
量子态变化过程:
∣x,y,0⟩⟶UCCNOT∣x,y,xy⟩=∣x,y,x∧y⟩
-
“或” 运算符为 ∨ ,真值表
用 Toffoli 门实现:
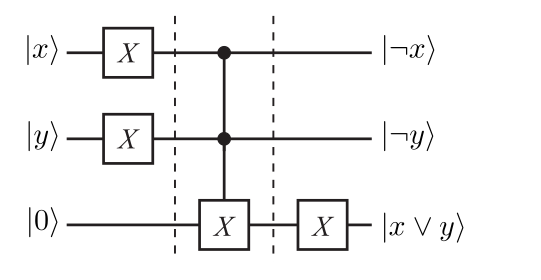
量子态变化过程:
∣x,y,0⟩⟶X⊗X⊗I⟶UCCNOT⟶I⊗I⊗X∣¬x,¬y,0⟩∣¬x,¬y,(¬x)∧(¬y)⟩=∣¬x,¬y,¬(x∨y)⟩∣¬x,¬y,x∨y⟩
Ps:“与非门”和“或非门”称为通用逻辑门,也可以生成所有经典逻辑门。
可逆计算
20 世纪中叶,人们发现计算机芯片的能耗会导致芯片发热,限制芯片集成度,进而影响计算机的运行速度。物理学家兰道尔发现,芯片能耗主要源于计算中的不可逆操作。
可逆计算(Reversible Computing),是一种计算模型,它的计算过程是可逆的。在这种计算模型中,使用的能量很低,熵的增加会最小化,换句话说,它几乎不会产生额外的热。
- 经典逻辑门多数是不可逆的,比如“与门”:
∧:{0,1}⊗2(0,0)(0,1)(1,0)(1,1)→{0,1}↦0↦0↦0↦1
当 x∧y=1 时,无法反推 (x,y) 取值。
- 量子电路中,量子门为酉矩阵,为可逆矩阵,运算自然可逆。
- 前边用 Toffoli 门实现不可逆的“与门”时,保留了前两个比特的信息,从而使计算可逆。
不可克隆定理
不可克隆定理指出:未知的量子态 ∣ψ⟩ 不可能通过酉变换复制信息。换言之,不存在满足如下形式的量子门,对任意 ∣ψ⟩ 成立:
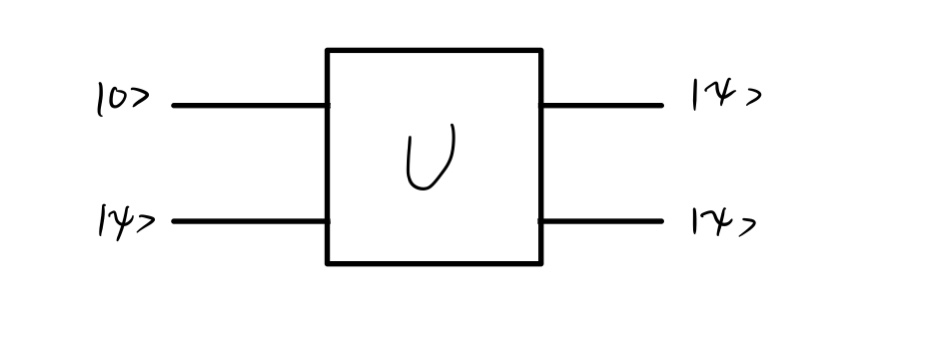
反证法,取正交的两个量子态 ∣ψ⟩,∣φ⟩,则:
U∣0,ψ⟩U∣0,φ⟩U∣0⟩21(∣ψ⟩+∣φ⟩)U∣0⟩21(∣ψ⟩+∣φ⟩)=∣ψ,ψ⟩=∣φ,φ⟩=21(U∣0,ψ⟩+U∣0,φ⟩)=21(∣ψ,ψ⟩+∣φ,φ⟩)=21(∣ψ⟩+∣φ⟩)(∣ψ⟩+∣φ⟩)=21(∣ψ,ψ⟩+∣ψ,φ⟩+∣φ,ψ⟩+∣φ,φ⟩)(1)(2)
比较 (1),(2) 系数,导出矛盾。
注记:
- 不可克隆定理指出:不存在酉变换,可以复制任意量子态的信息。
- 如果未知量子态取值局限在 ∣0⟩ 和 ∣1⟩,通过 CNOT 门就能复制。
∣i,0⟩⟶UCNOT∣i,i⊕0⟩=∣i,i⟩
- 类似还有“不可删除定理”,一种理解是:酉变换为可逆计算,因而信息不增不减。















