Julia 笔记系列：

唠唠闲话

本篇介绍 Julia 广播，向量化与代码性能，对应课程第四讲，主要内容如下：

课程讲义为 Pluto 文件，Pluto 的安装及介绍参看Julia 初学者指南(一) | 安装、配置及编译器。

广播

广播与 for 循环：

  1. Matlab 的广播本质是执行 for 循环，用起来快是因为使用 C 语言代码加速。
  2. 在 MATLAB/Python 这类语言中，for 循环执行效率低，广播运算允许我们将 for 循环的执行从一门缓慢的语言转移到一门高效的语言上执行。
  3. 对于 Julia 来说， 因为存在高效的 for 循环， 所以不用广播代码也很快， 使用广播只是可以让代码变得更简洁易读。

语法

  1. 当 X 与 Y 尺寸一致时， f.(X, Y) 等价于 map(f, X, Y)

    1
    2
    g(x, y) = x + y
    @show g.([1, 2], [3, 4])

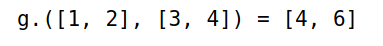
    深度截图_选择区域_20211104222059

  2. X 与 Y 的维数一致，且尺寸不同的维度有一个的长度为 1，此时长度为 1 的那个维度会被复制到尺寸一致。

    1
    2
    3
    4
    5
    @show x1 = reshape(1:6,2,3)
    @show y1 = reshape(1:2,2,1)
    @show g.(x1,y1)
    @show y2 = repeat(y1, 1, 3)
    @show g.(x1,y2)

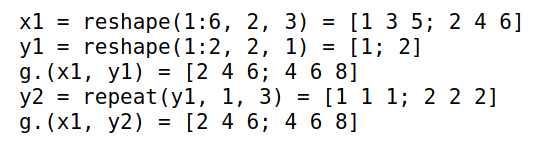
    深度截图_选择区域_20211104222906

  3. 高维及多变量的规则类似，维数相等时，广播要求各维度上，尺寸要么相同，要么取 1，这一来展开模式不会有歧义。

    1
    2
    3
    4
    5
    g(x,y,z) = z + y + z
    @show x1 = reshape(1:6,2,3)
    @show y1 = reshape(1:2,2,1)
    @show z1 = reshape(1:3,1,3)
    g.(x1,y1,z1)

    深度截图_选择区域_20211104223411

  4. 当 X 与 Y 的维数不一致时，维数小的矩阵补尺寸为 1 的维度后，再回到前边规则。

    1
    2
    3
    x4 = reshape(1:6,3,2) # 3x2
    y4 = [7, 8, 9] # 3 ---> 3x1
    @show g.(x4, y4) # 3x2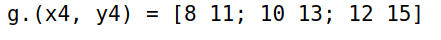

    深度截图_选择区域_20211104223748

注：计算矩阵元素之和时，用 for 循环逐列操作可以调用 @simd 并行加速；如果逐行操作使用 @simd 只没有加速效果。

调整尺寸

这两个函数常用于修改数据尺寸：

  • reshape: 在不改变内存顺序的情况下调整尺寸
  • permutedims: 交换维度 （同时会改变内存顺序）

  1. Julia 中的矩阵按列存储，查看方式

    1
    2
    3
    x = [1 2 3
         4 5 6]
    @show x[:]

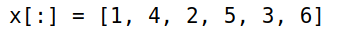
    深度截图_选择区域_20211104224037

  2. 换言之，二维数组存储顺序为

    a1,1→a2,1→⋯→an,1a1,2→a2,2→⋯→an,2⋯→⋯\begin{align*} &a_{1,1}\rightarrow a_{2,1} \rightarrow \cdots \rightarrow a_{n,1}\\ &a_{1,2}\rightarrow a_{2,2} \rightarrow \cdots \rightarrow a_{n,2}\\ &\qquad\cdots\rightarrow\cdots \end{align*}

  3. reshape 不改变内存顺序
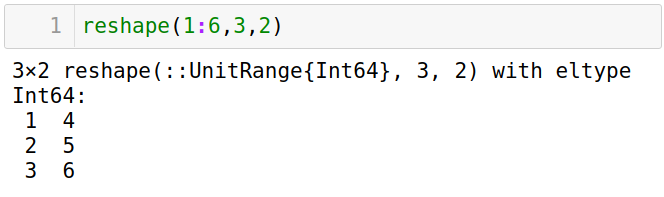
    深度截图_选择区域_20211104224319

  4. 用 reshape 查看高维数据的存储顺序，靠左维度先增大。
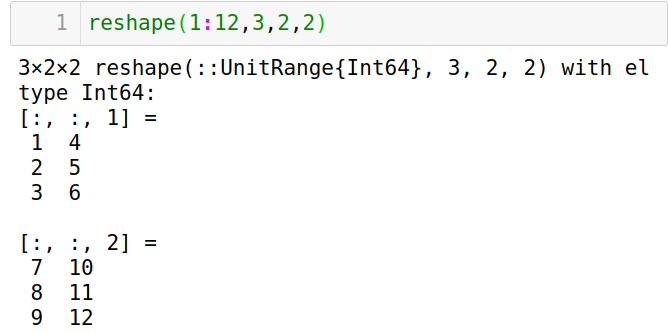
    深度截图_选择区域_20211104224828

  5. permutedims 交换维度，改变内存

    1
    2
    3
    x = [1 2 3
         4 5 6]
    permutedims(x,(2,1))

    深度截图_选择区域_20211104225600

代码性能

向量化编程

向量化编程就是尽可能避免显式 for 循环的代码，背后逻辑是为了尽可能将 for 循环从低效的 Python/MATLAB 端转移到高效的 C/Fortran 端， 从而尽可能少地触发这些动态语言的性能瓶颈。

  1. 我们将采用与广播类似规则的函数称为向量化函数，比如

    1
    2
    f(x::Real, y::Real) = x * y # 标量函数
    f(X::AbstractArray, Y::AbstractArray) = X .* Y # 向量化函数

  2. 向量化代码的问题

    • 向量化代码的实现需要底层 C/Fortran 代码进行支撑。如果你所关心的问题恰好没有人在 C/Fortran 下给出高效实现的话， 那么就需要你自己来做了。
    • 向量化代码的中间结果是数组而非标量， 会带来一定的额外内存开销。
    • 向量化代码可能会阻碍一些本可以进行的性能优化，或带来了一些不必要的代码。
    • 相比于标量代码来说，向量化代码既不容易阅读，也不容易写对。

Fused Dot

  1. A .* B .+ C 这种运算非常普遍，它背后有两种可能的实现方式

    1
    2
    3
    4
    5
    6
    ## 方法一，分两次运行
    tmp = A .* B
    tmp .+ C
    ## 方法二，使用一次广播
    f(a, b, c) = a * b + c
    f.(A, B, C)

  2. 第二种方式可以避免中间矩阵 tmp 的不必要内存开销，因此 Julia 提供了一个内置的 fused dots 机制：当整个运算都是点运算时，Julia 会试图构造类似 f 的标量形式的函数，然后对函数整体进行广播。同时，Julia 也提供了一个 @. 宏用来辅助代码书写。

  3. 举个例子，方法 1 运行时间长，方法 2，3 等价

    1
    2
    3
    4
    5
    6
    7
    8
    A,B,C = rand(100,100),rand(100,100),rand(100,100)
    muladd_v1(A, B, C) = A .* B + C
    # 以下两种写法是完全等价的
    muladd_v2(A, B, C) = A .* B .+ C
    muladd_v3(A, B, C) = @. A * B + C
    @btime muladd_v1($A, $B, $C)
    @btime muladd_v2($A, $B, $C)
    @btime muladd_v3($A, $B, $C);

    深度截图_选择区域_20211104231536

可以看到，第一种方法分配了更多内存，且计算用时更长。

延伸阅读
Dot Syntax for Vectorizing Functions
More Dots: Syntactic Loop Fusion in Julia

view

不必要的内存开销一直都是性能优化致力于解决的问题。

  1. 使用切片获取数据时，创建了新对象

    1
    2
    3
    4
    x = [1,2,3,4]
    y = x[1:2]
    y[1] = 0
    @show x y

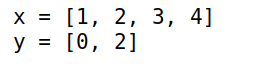
    20211104232221

  2. 使用宏 @view 可以引用原对象

    1
    2
    3
    4
    x = [1,2,3,4]
    y = @view x[1:2]
    y[1] = 0
    @show x y

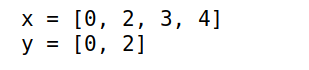
    深度截图_选择区域_20211104232308

  3. 当我们不需要修改数据时，使用 @veiw 可以减少内存开销，继而加快运行速度。

Ps：Python 中切片也是创建新对象，不过没有类似 Julia 的处理工具。