基本假设，数学化与量子态 | 量子系列之一

量子计算系列：

• 『量子系列之零 | 量子计算概述』
• 『量子系列之一 | 基本假设，数学化与量子态』
• 『量子系列之二 | Bloch 球与泡利矩阵』
• 『量子系列之三 | 量子门与量子电路』
• 『量子系列之四 | 量子传输与密钥分发』

---

唠唠闲话

量子系列第一篇，内容如下：

• 量子力学基本假设(Fundamental Postulates)
• 数学化：叠加，测量和时间演化
• 量子态：叠加态，纯态与混合态，分离态与纠缠态

其中数学化是量子电路和量子算法的基础。

Ps：系列直到 shor 算法实现基本只用线性代数知识。

---

基本假设

量子力学的假设，跟数学体系中的公理类似，这些设定本身无法从理论上进行严格证明，但是根据它们，从这几条假设出发，能够推导出量子力学的全部内容。

波函数假设

微观体系的运动状态由相应波函数 $\vert\psi\rangle$ 描述。

演化假设

微观体系的运动状态波函数随时间变化的规律遵从薛定谔方程。

延伸：波函数与薛定谔方程，以及一文读懂薛定谔方程。

算符假设

量子力学中力学量用厄米(Hermitian)算符表示。
在微观系统中，系统的全部信息(位置，动量等)都包含在波函数中，如果改变体系(即波函数)的状态，在数学上是对波函数进行变换操作，给波函数施加操作的便是物理量，那么物理量需要用算符表示(因为只有某种算符能够操作函数)。物理量也就是可观测量一定是有实际意义的，不可能是一个虚数，所以物理量对应的算符一定是厄米的，即转置复共轭为本身。

测量假设

测量力学量时，测量结果一定是本征值之一，测量以后状态波函数塌缩到本征态。这是量子测量和经典测量本质的区别，它破坏了原有状态。

全同性假设

全同的多粒子体系的波函数对于任意一对粒子交换而言具有对称性：玻色子系的波函数是对称的，费米子系的波函数是反对称的。
在量子系统中，存在内禀属性完全相同的粒子，对任意两个这样的粒子进行交换不会改变系统的状态。

参考文章
知乎：量子力学是建立在一系列的假设上的吗？
知乎：量子力学五个基本假设如何提出？
知乎：量子力学究竟有几个基本假设？
B 站：量子力学的五个基本假设

---

下边讨论使用狄拉克符号，建议先看系列第 0.5 篇：狄拉克符号 | 量子系列之0.5。

数学表述

量子力学基本假设的数学化，有三个重要概念：量子态，测量，时间演化，这些是量子电路和量子算法的数学基础。

前置知识

讨论前，先回顾线性代数的结论。

1. 记 $A^\dagger$ 为矩阵 $A$ 的 Hermitian 转置

   • 酉矩阵(unitary matrix)：$A^\dagger A=I$
   • 埃尔米特矩阵(Hermitian matrix)：$A^\dagger=A$
   • 反埃尔米特矩阵(skew-Hermitian matrix)：$A^\dagger+A=O$
   • 正规矩阵(normal matrix)：$A^\dagger A=AA^\dagger$

2. 酉矩阵，埃尔米特矩阵和反埃尔米特矩阵都是正规矩阵，是欧式空间正交矩阵，对称矩阵和反对称矩阵在复数域上的推广。

3. 称矩阵 $A$ 和 $B$ 酉相似，若存在酉矩阵 $U$ ，使得 $A=U^\dagger BU$ 。

4. 称 $A$ 可酉对角化(unitarily diagonalizable)，若 $A$ 酉相似于复对角阵。

5. 正规矩阵的谱分解(spectrum decomposition)：

   • $A$ 可酉对角化当且仅当 $A$ 为正规矩阵，此时
   • $A=UDU^\dagger$， $U$ 为酉矩阵，$D$ 为复对角阵
   • 设 $U=(\alpha_1,\cdots,\alpha_n)$， $diag(D)=(\lambda_1,\cdots,\lambda_n)$，则
     • $\{\alpha_i\}_{i=1}^n$ 为一组标准正交基
     • $A=\sum\limits_{i=1}^n \lambda_i\alpha_i\alpha_i^\dagger$
   • 令 $P_i=\alpha_i\alpha_i^\dagger$ 为投射算子， $A=\sum\limits_{i=1}^n\lambda_iP_i$ 称为矩阵 $A$ 的谱分解。

6. 狄拉克符号下，设 $A$ 为 $Hermitian$ 算符，则有谱分解

   • $A=\sum\limits_{i=1}^n\lambda_iP_i$， $P_i=\vert\alpha_i\rangle\langle\alpha_i\vert$ 为投射算子
   • 记号方便，一般写为 $A=\sum\limits_{i=1}^n\lambda_i\vert\lambda_i\rangle\langle\lambda_i\vert$
   • 注意：括号内 $\lambda_i$ 为向量，括号外 $\lambda_i$ 为数值

量子态

1. 维基释义：
   
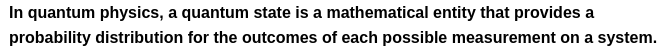
   简言之，量子态是一个数学量，它提供任一可观测量的测量结果的概率分布。

2. 纯态(pure state)是希尔伯特空间 $\mathcal{H}$ 中的复射线

   $$\{c\cdot\vert\psi\rangle\mid c\in\mathbb{C}\ and\ c\neq 0\}$$

   用向量 $\vert\psi\rangle$ 表示，一般还要求归一化条件

   $$\langle\psi\vert\psi\rangle=1$$

3. 叠加态(superposition)：
   若纯态 $\vert\psi\rangle=\sum\limits_{i=1}^nc_i\vert\psi_i\rangle$ 其中 $\vert\psi_i\rangle$ 相互正交，则称 $\vert\psi\rangle$ 处于 $\{\vert\psi_i\rangle\}_{i=1}^r$ 这 n 种状态的叠加。

注记：

• $\vert\psi\rangle$ 代表集合等价类 $\{e^{i\alpha}\vert\psi\rangle\vert\alpha\in\mathbb{R}\}$
• 相差幅角的向量表示同一个纯态：
  $\vert\psi\rangle=e^{i\alpha}\vert\psi\rangle,\ \alpha\in\mathbb{R}$
• 相差的幅角称为整体相位(overall phase)
• 特别注意，虽然 $\vert\psi\rangle=e^{i\alpha}\vert\psi\rangle$，但一般来说

$$\vert\psi\rangle+\vert\varphi\rangle\neq e^{i\alpha}\vert\psi\rangle+\vert\varphi\rangle$$

测量

波恩准则

测量遵循波恩准则(born rule)，维基释义：

测量表述及计算公式

1. 可观测量(observable) 与叠加态

   • 可观测量是一个物理量，可以简单理解为 Hermitian 算子 $A$，一般与量子态 $\vert\psi\rangle$ 一起给出；
   • 做谱分解 $A=\sum\limits_{i=1}^n \lambda_i\vert\psi_i\rangle\langle\psi_i\vert$ ，得正交基 $\{\vert\psi_i\rangle\}_{i=1}^n$ ；
   • $\vert\psi\rangle$ 做正交分解 $\vert\psi\rangle=\sum\limits_{i=1}^nc_i\vert\psi_i\rangle$，并称 $\vert\psi\rangle$ 为这 n 个状态的叠加态。

2. 波恩准则给出下边表述：

   • 算子 $A$ 的每次测量结果为特征值 $\{\lambda_i\}_{i=1}^n$ 中的一个
   • 每次测量，得到 $\lambda_i$ 的概率为 $\vert c_i\vert^2$，测量后量子态相应塌缩为 $\vert\psi_i\rangle$

3. 记 $\langle A\rangle$ 为可观测量 $A$ 的测量结果的期望值， 下边推导公式 $\langle A\rangle=\langle\psi\vert A\vert\psi\rangle$：

   1. 由期望计算公式，得 $\langle A\rangle=\sum\limits_{i=1}^n\lambda_i\vert c_i\vert^2$
   2. 由 $A=\sum\limits_{k=1}^n \lambda_k\vert\psi_k\rangle\langle\psi_k\vert$ ，得

   $$\langle \psi_i\vert A\vert\psi_j\rangle = \sum\limits_{k=1}^n \lambda_k\langle\psi_i\vert\psi_k\rangle\langle\psi_k\vert\psi_j\rangle=\lambda_i\delta_{ij}$$

   3. 最后

      $$\begin{align*} \langle\psi\vert A\vert\psi\rangle&=\sum\limits_{i,j}^n\langle c_i\psi_i\vert A\vert c_j\psi_j\rangle\\ &=\sum\limits_{i,j}^nc_i^*c_j\langle \psi_i\vert A\vert\psi_j\rangle\\ &=\sum\limits_{i=1}^nc_i^*c_i\lambda_i=\langle A\rangle \end{align*}$$

注记：

• 特别强调，测量的两个事实，一是依概率测得 $A$ 的特征值 $\lambda$；二是量子态塌缩为 $\vert\lambda\rangle$ 。
• 测量结果（特征值）和塌缩结果与算子 $A$ 有关；测量的概率则与量子态 $\vert\psi\rangle$ 有关。
• “塌缩”是量子算法的构造技巧之一，比如 Simon algorithm。

时间演化

量子力学的态是随时间所改变的，纯态由波函数 $\vert\psi(t)\rangle$ 描述，随时间变化的规律遵从薛定谔方程。

$$\begin{align*} i\hbar\frac{\partial\vert\psi\rangle}{\partial t}&=(-\frac{\hbar^2}{2m}\nabla^2+\mathrm{V})\vert\psi\rangle=\hat{H}\vert\psi\rangle \end{align*}$$

其中：

• $i$ 为虚数单位；
• $\hbar=\frac{h}{2\pi}$ 为约化普朗克常数；
• $\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)$ 为梯度算子；
• $\mathrm{V}=\mathrm{V}(x,y,z)$ 为体系的势能分布，取决于具体的物理形式
• $\vert\psi\rangle=\vert\psi(t)\rangle$ 为波函数
• $\hat{H}=(-\frac{\hbar^2}{2m}\nabla^2+\mathrm{V})$ 为哈密顿算子(Hamiltonian)

方程解

1. 当哈密顿算子 $\hat{H}$ 与时间无关时，方程解为

   $$\begin{align*} \vert\psi(t)\rangle&=e^{\frac{-i\hat{H}t}{\hbar}}\vert\psi(0)\rangle\\ &=U(t)\vert\psi(0)\rangle \end{align*}$$

   其中 $U(t)=e^{\frac{-i\hat{H}t}{\hbar}}$ 为时间演化算符。

2. 当哈密顿算子 $\hat{H}$ 随时间改变时，方程解为

   $$\begin{align*} \vert\psi(t)\rangle&=\mathcal{T}exp\left[\frac{-i}{\hbar}\int_{0}^{t}\hat{H}(t)dt\right]\vert\psi(0)\rangle\\ &=U(t)\vert\psi(0)\rangle \end{align*}$$

   其中 $\mathcal{T}$ 为时序算符。

注记：

• 算符 $U(t)$ 为酉算符，保持 $\vert\psi(t)\rangle$ 的归一化性质；
• 量子态可能随时间改变或者不变；
• 不变的例子：波函数 $\vert\psi(t)\rangle=\frac{e^{iwt/2}}{\sqrt{2}}\begin{pmatrix}1\\ 1\end{pmatrix}$，整体相位随时间变化，但量子态不变；
• 改变的例子：Rabi oscillation，用于构造量子门。

量子电路和量子算法中，将时间演化算符 $U(t)$ 简化为酉矩阵，后续讨论只用到线性代数知识，不涉及解微分方程。

---

量子态

前边提到，量子态是一个数学量，它提供任一可观测量的测量结果的概率分布。简单说，量子态是描述测量性质的数学量。

初学有几个概念容易混淆：纯态，混合态，叠加态，纠缠态，分离态。本节给出它们的数学定义，并从测量性质理解和区分这些概念。
总的关系如下：

1. 量子态分两类，能写成向量形式 $\vert\psi\rangle$ 的称为纯态；否则称为混合态。
2. 叠加态是纯态中的概念，当正交基给出时（比如测量 $A$ ），纯态看成这组正交基的叠加态。
3. 纯态分为“纠缠态”(entangled)和“分离态”(separable)，能拆为张量乘积的是分离态，否则称为纠缠态。
4. 混合态分为“不相关态”(uncorrelated)，“分离态”(separable)和“不可分离态”(inseparable)，用密度矩阵定义。

纯态和叠加态

1. 测量信息用向量表示的量子态称为纯态，用归一化向量 $\vert\psi\rangle$ 表示。

2. 叠加态是纯态的一个描述，做正交分解 $\vert\psi\rangle=\sum\limits_{i=1}^nc_i\vert\psi_i\rangle$ 时，我们称 $\vert\psi\rangle$ 处于 $\{\vert\psi_i\rangle\}_{i=1}^n$ 这 n 种状态的叠加。

特别说明，量子比特都是纯态，学习量子电路和量子算法把纯态概念理解清楚就够了。

测量性质

1. 给定可观测量 $A=\sum\limits_{i=1}^n \lambda_i\vert\lambda_i\rangle\langle\lambda_i\vert$ 和纯态 $\vert\psi\rangle=\sum\limits_{i=1}^nc_i\vert\lambda_i\rangle$；
2. 每次测量，以 $\mid c_i\mid^2$ 概率测得特征值 $\lambda_i$ ，同时量子态塌缩为 $\vert\lambda_i\rangle$；
3. 测量期望 $\langle A\rangle=\langle\psi\vert A\vert\psi\rangle$。

Ps：纯态可以看成特殊的混合态，下边关于混合态的讨论也适用于纯态。

混合态

量子系统中，不能写为纯态形式的量子态称为混合态(mixed state)。我们先表述其测量性质，再引入密度矩阵这一数学表示。

测量性质

1. 混合态是多个纯态的混合：以 $p_i$ 概率处在状态 $\vert\psi_i\rangle$；
2. 考虑可观测量 $A$，每次测量，有 $p_i$ 概率在测 $\vert\psi_i\rangle$，测得 $\langle \psi_i\vert A\vert\psi_i\rangle$；
3. 测量期望

   $$\begin{align*} \langle A\rangle&=\sum_{i=1}^rp_i\langle \psi_i\vert A\vert\psi_i\rangle\\ &=\sum_{i=1}^rp_iTr(\vert\psi_i\rangle\langle \psi_i\vert A)\\ &=Tr(\sum_{i=1}^rp_i\vert\psi_i\rangle\langle \psi_i\vert A)\\ &=Tr(\rho A) \end{align*}$$

   其中 $Tr$ 为取迹函数，$\rho=\sum\limits_{i=1}^rp_i\vert\psi_i\rangle\langle \psi_i\vert$
   等号一为期望定义，等号二用了迹等式 $Tr(AB)=Tr(BA)$，等号三用了迹运算的线性性。

密度矩阵

1. 根据上边推导，我们给出混合态的密度矩阵定义：

   1. 设混合态以 $p_i$ 概率处在状态 $\vert\psi_i\rangle$；
   2. 用 $\rho=\sum\limits_{i=1}^rp_i\vert\psi_i\rangle\langle \psi_i\vert$ 表示该混合态，并称 $\rho$ 为该混合态的密度矩阵；
   3. 对可观测量 $A$ ，测量期望为 $\langle A\rangle=Tr(\rho A)$；
   4. $\mathcal{H}$ 上，密度矩阵构成的集合记为 $\mathcal{S}(\mathcal{H})$。

2. 特别地，纯态 $\vert\psi\rangle$ 可写成密度矩阵形式： $\rho=\vert\psi\rangle\langle\psi\vert$ 。

3. 密度矩阵 $\rho$ 的相关性质：

   1. 矩阵 $\rho$ 为某一混合态的密度矩阵 $\Leftrightarrow$ $\rho$ 为半正定的 Hermitian 矩阵，且 $Tr(\rho)=1$；
   2. 纯态刻画

   $$\begin{align*} \rho\ \ is\ a\ pure\ state &\Leftrightarrow rank(\rho)=1\\ &\Leftrightarrow \rho^2=\rho\\ &\Leftrightarrow Tr(\rho^2)=1 \end{align*}$$

   1. 设密度矩阵的秩 $rank(\rho)= r$ ，则存在 $r$ 个纯态 $\{\vert\psi_i\rangle\}_{i=1}^r$，使得 $\rho=\sum\limits_{i=1}^rp_i\vert\psi_i\rangle\langle \psi_i\vert$；但注意纯态 $\{\vert\psi_i\rangle\}_{i=1}^r$ 的取法不唯一。

注记：

• 注意区分密度矩阵与测量算子，二者均为矩阵形式，但根据语境， $\vert\psi\rangle\langle\psi\vert$ 可能是投射算子，也可能是密度矩阵。
• 纯态的向量形式 $e^{i\alpha}\vert\psi\rangle$ 写法不唯一，但

$$\rho=e^{i\alpha}e^{-i\alpha}\vert\psi\rangle\langle\psi\vert=\vert\psi\rangle\langle\psi\vert$$

纯态的密度矩阵写法唯一。

• 同样地，混合态的“纯态概率和”表述不唯一，但密度矩阵写法唯一。
• 特别注意，时间演化算子 $U(t)$ 作用在向量 $\vert\psi\rangle$ 上的结果为 $U(t)\vert\psi\rangle$，即线性变换；其作用在密度矩阵 $\rho$ 上的结果为 $U(t)\rho U(t)^\dagger$，即酉相似变换。

Ps：单量子系统中，量子态与 Bloch 球有精巧的对应。与几何结合在一起，可导出有趣的结论，参看系列第二篇

分离态与纠缠态

分离态和纠缠态是两量子系统张量下的概念，设 $\mathcal{H}_1$ 和 $\mathcal{H}_2$ 是两个量子系统，它们张量得到空间

$$\mathcal{H}=\mathcal{H}_1\otimes\mathcal{H}_2=\{\sum\limits_{k=1}^r\vert\psi_{1,k}\rangle\otimes\vert\psi_{2,k}\rangle :\ \vert\psi_{1,k}\rangle\in \mathcal{H}_1,\ \vert\psi_{2,k}\rangle\in\mathcal{H}_2\}$$

称 $\vert\psi\rangle\in\mathcal{H}$ 为分离态，若存在 $\vert\psi_1\rangle\in\mathcal{H}_1$ 和 $\vert\psi_2\rangle\in\mathcal{H}_2$ 使得 $\vert\psi\rangle=\vert\psi_1\rangle\vert\psi_2\rangle$，否则称其为纠缠态。

混合态中的分离概念

大致知道即可，暂时用不到。
设 $\rho$ 为 $\mathcal{H}=\mathcal{H}_1\otimes\mathcal{H}_2$ 上的密度矩阵，相关定义如下：

1. 称 $\rho$ 为不相关态，若存在 $\rho_1\in\mathcal{S}(\mathcal{H}_1)$ 和 $\rho_2\in\mathcal{S}(\mathcal{H}_2)$ ，使得$\rho=\rho_1\otimes\rho_2$。
2. 称 $\rho$ 为分离态，若存在 $\rho_{1,k}\in\mathcal{S}(\mathcal{H}_1)$ 和 $\rho_{2,k}\in\mathcal{S}(\mathcal{H}_2)$ ，使得 $\rho=\sum\limits_{k}\rho_{1,k}\otimes\rho_{2,k}$
3. 其他情形称 $\rho$ 为不分离态。

延伸：纯态和混合态的相互转化

• $\mathcal{H}_1\otimes\mathcal{H}_2$ 上的纯态取偏迹(partial trace)，可能得到 $\mathcal{H}_1$ 上的混合态。
• 反之， $\mathcal{H}_1$ 的混合态总能由某一张量空间 $\mathcal{H}_1\otimes\mathcal{H}_2$ 的纯态取偏迹得到，这一过程称为混合态的纯化(purification)。

---

参考资料
教材：Nakahara 第1，2章
维基：量子态，玻恩准则，可观测量