QR Code Learning Notes (8) | Project Summary

In this article, we will talk about two things:

• What does a QR code consist of, and what is the theory behind it?
• General usage of QRCoders.jl and QRDecoders.jl

These packages are created as main works of the OSPP’22 project. They are built following the ISO/IEC 18004:2015 standard, the excellent tutorial and the wikiversity-entry. Therefore, images generated by QRCoders.jl can be decoded by a common QR code decoder or by QRDecoders.jl.

For more introduction, please refer to the announcement in Julia Discourse.

Decomposition of QRCodes

There are two parameters that are crucial to the capacity of a QR code: Version and Error correction level:

• The size of the QR code with version k(1-40) is 17+4k x 17+4k
• QR codes have four error correction levels, L, M, Q, H. Higher the error correction level needs more error correction bits, thus the capacity of the QR code will be smaller.

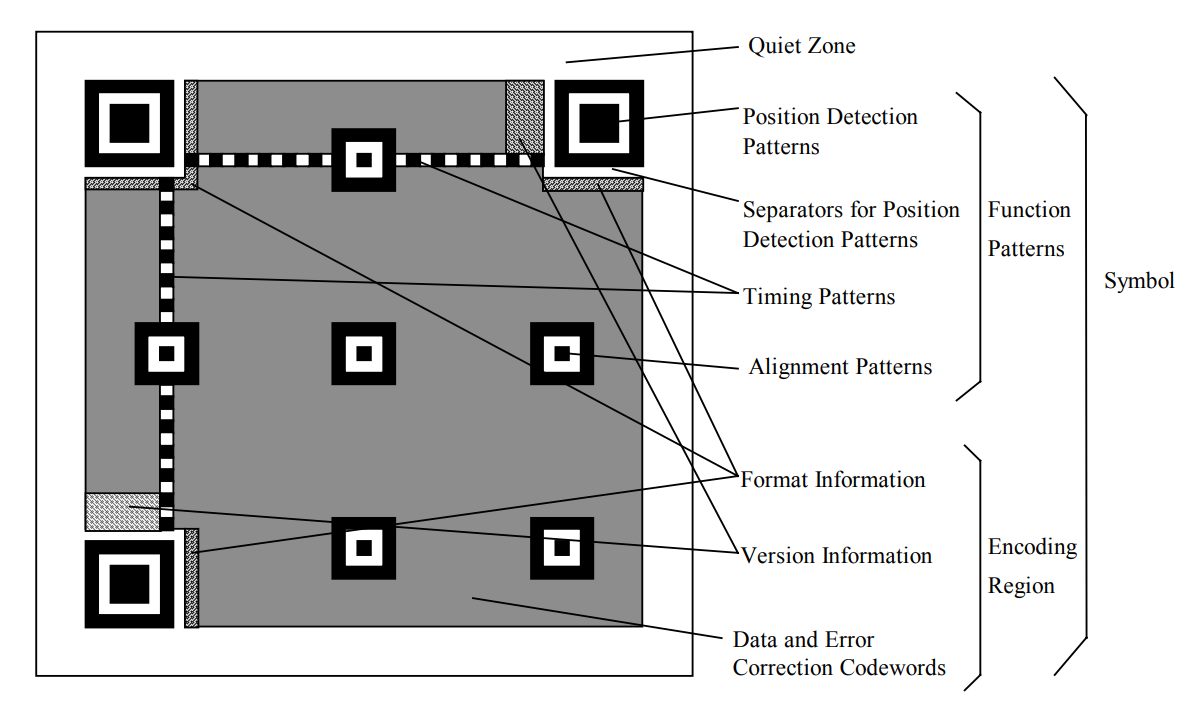
The following figure is a QR code with version 7, which is mainly divided into Function Patterns and Encoding Region.

1. Function Patterns: used for image detection
   

2. Encoding Region, including format information, version information and encoding data

   • Format information is consisted of error correction level and mask pattern, 15 bits in total
     
   • Version information, only exists when version ≥7, 18 bits in total
     
   • Encoding data: the remaining empty space stores encoding data

Encoding process

The encoding process of QRCodes is a bit complicated, but we can decompose it into several steps:

1. Choose the best encoding mode from the five modes: Numeric, Alphanumeric, Byte, Kanji and UTF8, and then encode the data into bytes.

2. Split the message bytes into several small blocks, each block is associated with an error correction block.

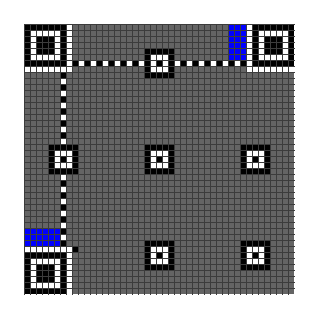
3. Fill in the Function Patterns and Encoding Region.
   
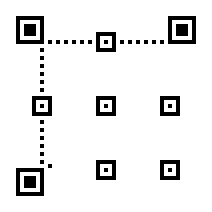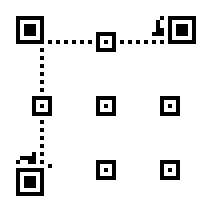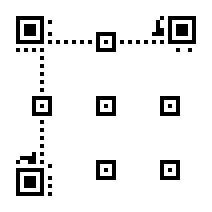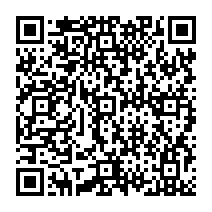
   The Encoding Region is filled from right to left.
   

4. Apply different masks to the QR matrix, and pick up the one with lowest penalty score.

5. Mask patterns are used to make the QR code more scannable. As an example, the following case is designed to confuse the scanner.
   

Decoding is the reverse process of encoding. The steps are:

• Locate the image
• Read the format area to get the mask pattern
• Apply the mask to restore the original QR matrix
• Extract the encoded data
• Error correction for the encoded data
• Decode the original string from the encoded data

The most difficult parts are locating and error-correction.

Theory behind error correction

An example

During data transmission, some errors may occur, such as 1 is transmitted as 0 or some data is lost. Therefore, error correction code is introduced to improve the robustness of the data transmission.

There are three applications of error correction codes: error detection, fill erased data and error correction.

In essence, error correction codes introduce more space to represent a small data set. The redundant information improves the error tolerance of the data. We use an example to illustrate this process.

Suppose Alice wants to send $x\in\{0,1\}$ to Bob, in order to increase the error tolerance, Alice uses the following encoding scheme

$$\begin{align*} x = 0 \quad &\rightarrow &\quad y=000 \\ x = 1 \quad &\rightarrow &\quad y=111 \end{align*}$$

Now Alice sends the encoded $y$ to Bob

• Error correction: suppose at most 1 bit error occurs during transmission, such as $000\rightarrow 010$, obviously Bob can decode $010$ as $0$, thus correct the error
• Error detection: suppose at most 2 bit errors occur during transmission, such as $000\rightarrow 110$, although Bob cannot determine whether the original information is $0$ or $1$, he can determine whether an error occurs during transmission
• fill erased data: suppose 2 bits are lost during transmission, such as $000\rightarrow 0**$, obviously Bob can fill in the missing data to get $000$

Coding Theory

The example above uses a linear code with Hamming distance 3. In general, let $C$ be a linear code with Hamming distance $d$, then

• $C$ can detect at most $e\leq d-1$ errors
• $C$ can fill at most $e\leq d-1$ erased data
• $C$ can correct at most $e\leq \lfloor\frac{d-1}{2}\rfloor$ errors, i.e. $2e\leq d-1$

The Hamming distance is the minimum number of bits that need to be changed to convert one code to another, for example, the Hamming distance between $000$ and $010$ is 1, and the Hamming distance between $000$ and $110$ is 2.

Let’s understand this theorem through an image. The original information is a set of dots, and we use larger spheres to represent these dots. The Hamming distance of a code is the minimum distance between dots. When the number of errors is within half of the distance, we can always correct them.

ReedSolomon is one of the most commonly used error correction codes. Moreover, it meets the following criterias:

• Stronger error handling ability
• Smaller redundant information as possible
• Efficient encoding and decoding algorithms

General usage

1. Create a QR code

   using QRCoders
   # creat a QRCode object
   code = QRCode("Hello World!")
   # use the object to creat a QR code
   qrcode(code)
   # equivalently, use the function directly
   qrcode("Hello world!")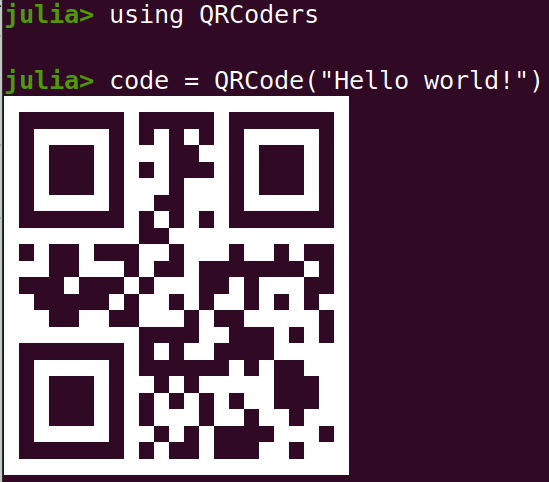

   

2. Export pictures from QR codes

   # direct method
   exportqrcode("Hello world!", "hello.png")
   # use the object `QRCode`
   exportqrcode(code)

3. Export animated GIF from QR codes

   exportqrcode(["Hello", "Julia", "!"], "hello.gif")

   

4. Specified parameters

   code = QRCode("Hello World!", version=1, eclevel=Low(), mode=UTF8(), mask=0, width=2)

5. Decode message

   using QRDecoders, QRCoders, Test
   # decode message from QR code matrix
   code = QRCode("Hello World!", width=0)
   mat = qrcode(code)
   info = qrdecode(mat)
   @test info.message == "Hello World!"
   @test info == code
   
   # decode message from pictures
   exportqrcode("Hello World!", "test.png")
   info = qrdecode("test.png")
   @test info.message == "Hello World!"

Special QR codes

1. Unicode plot

   using QRCoders
   unicodeplot("Hello World!") # via UnicodePlots.jl
   # plot using Unicode characters `['█', '▀', '▄', ' ']`
   unicodeplotbychar("Hello World!") |> println 

   This idea is suggested by notinaboat in the issue#25

2. pixel drawing: Plot image in a QR code

   using TestImages, ImageTransformations, FileIO, ColorTypes
   # read image
   img = testimage("cameraman")
   code = QRCode("HELLO WORLD", version=20)
   inlen = qrwidth(code) - 2 * code.border - 15
   bitimg = .!(Bool.(round.(Gray.(imresize(img, (inlen, inlen))))))
   # draw image inside the QR code
   mat = imageinqrcode(code, bitimg, rate=0.9)
   # file export
   mat |> exportbitmat("cameraman.png")

   

Note that this is not a simple padded image, but is plotted using error correction and free bits. So it is scannable by a normal QR code reader. The idea of plot using free bits and error correction is inspired by ibukisaar.

Other styles are on the way, welcome to contribute!

---

Final words

Styles of a QR code has a creative room that beyond one’s imaginations.

However, due to my limited time and energy, I am currently focusing on the implementation of pixel drawing only. Feel free to give your valuable suggestions to help improve this package!