二维码学习笔记(五) | 数据掩码与版本信息

二维码笔记系列：

唠唠闲话

本节是生成二维码的最后一步，内容包括数据掩码的生成，以及二维码的版本信息的填充。

数据掩码

概述

既然模块已放置在矩阵中，则必须确定最佳掩码图案。掩模图案根据特定规则改变哪些模块是暗的，哪些是亮的，此步骤的目的是修改二维码码，以使二维码码阅读器尽可能容易地扫描
二维码规范定义了 8 种可应用于二维码的掩码图案，设 x,y 分别代表模块的横纵坐标：

掩码比特，记 x,y 分别为二维码矩阵的行列坐标

比特信息（十进制）	掩码规则
`0`	`(x + y) % 2 == 0`
`1`	`x % 2 == 0`
`2`	`y % 3 == 0`
`3`	`(x + y) % 3 == 0`
`4`	`(x / 2 + y / 3) % 2 == 0`
`5`	`(x * y) % 2 + (x * y) % 3 == 0`
`6`	`((x * y) % 2 + (x * y) % 3) % 2 == 0`
`7`	`((x + y) % 2 + (x * y) % 3) % 2 == 0`

掩码图案仅应用于数据模块和纠错模块，换句话说：
- 不要屏蔽功能模式（探测图案、时序图案、分隔符、对齐图案）
- 不屏蔽保留区（格式信息区、版本信息区）

最佳掩码图案

将掩码图案应用于二维码矩阵后，将根据二维码规范中定义的四个评估条件对其进行惩罚评分。二维码编码器必须应用所有八个掩码模式并评估每一个，罚分最低的掩码图案将被用于最终输出。
特别注意：即使屏蔽仅应用于数据和纠错模块，也会评估整个矩阵（包括功能图案和保留区域）。
四种出发规则可概括如下：
- 每组五个或更多相同颜色的模块在一行（或列）中给予二维码惩罚
- 矩阵中相同颜色模块的每个 2x2 区域对二维码进行惩罚
- 如果存在看起来与查找器图案相似的图案，规则 3 会给 QR 码一个很大的惩罚
- 如果超过一半的模块是暗或亮的，则对 QR 码进行惩罚，差异越大，惩罚越大

评估条件

评估条件1：逐行检查每一行，如果有五个连续的相同颜色的模块，则罚分加 3。如果在前五个之后还有更多相同颜色的模块，则每增加一个相同颜色的模块就加 1。之后，用同样方法处理列，并将两部分分数求和，例如
评估条件2：寻找至少 2x2 模块或更大的相同颜色的区域。二维码规范说，对于一个大小为 m × n 的纯色块，罚分是 3 × (m - 1) × (n - 1)。但是二维码规范并没有规定当有多种分割纯色块的方式时如何计算罚分！因此，与其寻找大于 2x2 的纯色块，不如简单地将 QR 码中相同颜色的每个 2x2 块的罚分加 3，确保计算重叠的 2x2 块。例如，相同颜色的 3x2 块应计为两个 2x2 块，一个重叠另一个。

注意探测图形也要计算进去，实际上这并不会影响评估结果。
评估条件3：寻找某一侧有四个光模块的暗-亮-暗-暗-暗-亮-暗模式。换句话说，它会查找以下两种模式中的任何一种

每发现一个图案扣 40 分，例如下图扣 80 分
评估条件4：最终评估条件基于亮模块和暗模块的比率，按以下步骤进行
- 计算矩阵中的模块总数
- 计算矩阵中有多少个暗模块
- 计算矩阵中深色模块的百分比
$r = \frac{darkmodules}{totalmodules} \times 100$
- 确定 $r$ 邻近的两个为 5 倍数的百分比。例如，当 $r=43$ 是，邻近的两个分别为 $40$ 和 $45$
- 计算这两个百分比与 $50$ 的差值，并将结果除以 5，例如
$\frac{|40 - 50|}{5} = \frac{10}{5}=2,\frac{|45 - 50|}{5}=\frac{5}{5} = 1$
- 取两个数字中最小的一个并乘以 10，作为罚分，比如这里取 1，罚分为 10.
- 再看一个例子，计算得到 $r=\frac{213}{441} * 100\approx 48.2993$ ，相邻百分比为 45，50，罚分为 0。
注：邻近的两个比例一般用 floor, ceil 来确定
将四个罚分相加，总分是二维码的总罚分，取罚分最低的掩码图案应用于二维码上，如下图

格式和版本信息

二维码的最后一步是创建格式字符串和版本字符串，并将它们放置在二维码中的正确位置，下边解释这一过程。

格式字信息

二维码有 4 个纠错级别和 8 个掩码模式，因此有 32 种可能的格式信息，这些按格式版本信息表进行编码。

格式字符串总长度为 15 比特，总的生成过程：
- 创建 5 位字符串，记录纠错级别和掩码信息
- 以 10100110111 为生成元多项式，生成 10 个纠错位
- 将得到的 15 位字符串与 101010000010010 异或
纠错等级对应的 2 比特

纠错等级比特信息

L 01

M 00

Q 11

H 10

需注意的是，纠错等级的比特不是按顺序递增的

纠错等级	比特信息
`L`	`01`
`M`	`00`
`Q`	`11`
`H`	`10`

和纠错编码类似，用带余除法对 5 位比特生成 10 个纠错位

## Julia 代码
function qrformat(fmt::Int)
   0 ≤ fmt ≤ 31 || throw("format code $fmt should be no less than 0 and no greater than 31")
   err = fmt << 10 # error correction code
   g = 0x537 # generator polynomial(= 0b10100110111 in binary)
   for i in 4:-1:0
      if !iszero(err & (1 << (i + 10)))
            err ⊻= g << i
      end
   end
   fmt << 10 ⊻ err ⊻ 0x5412 # mask(= 0b101010000010010 in binary)
end

举个例子，设纠错等级为 L 掩码为 4
- 5 位格式字符串 01 100
- 计算得到纠错位 1000111101
- 二者拼接得到 011000111101
最后将这 15 位从左到右，按下图顺序填入格式字符串区域

版本信息

注：这一步实际上发生在掩码模式之前，但是为了方便，和格式信息一起讨论。

如果二维码是第 7 版或更高版本，则必须在二维码的左下角和右上角包含一个 18 位的版本信息字符串。（有关所有可能的版本信息字符串的完整列表，请参阅格式版本信息表）
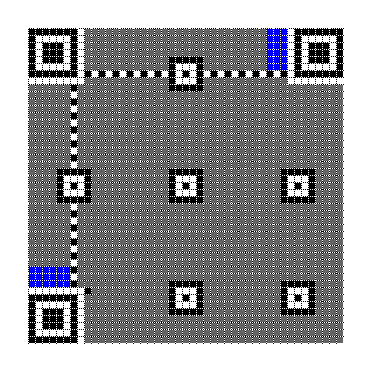
版本信息区域是下图中显示的 6x3 蓝色矩形。无论二维码有多大，版本信息都放在探测图案旁边。

二维码规范要求版本信息串使用 (18,6) Golay Code。其字符总长为 18 位，由 6 个数据位和 12 个纠错位组成，具体地，取生成元多项式 x12 + x11 + x10 + x9 + x8 + x5 + x2 + 1

## Julia 代码
function qrversion(ver::Int)
   7 ≤ ver ≤ 40 || throw("version code $ver should be no less than 7 and no greater than 40")
   # error correction code
   err = ver << 12
   # generator polynomial(= 0b1111100100101 in binary)
   g = Int(0x1f25) # use Int(0x1f25) to avoid overflow
   for i in 5:-1:0
      if !iszero(err & (1 << (i + 12)))
            err ⊻= g << i
      end
   end
   return ver << 12 ⊻ err
end

位于左下角的情形，使用以下顺序

1 2 3 4 5 6

00 03 06 09 12 15

01 04 07 10 13 16

02 05 08 11 14 17
位于右上角的情形，使用以下顺序

1 2 3

00 01 02

03 04 05

06 07 08

09 10 11

12 13 14

15 16 17

1	2	3	4	5	6
00	03	06	09	12	15
01	04	07	10	13	16
02	05	08	11	14	17

1	2	3
00	01	02
03	04	05
06	07	08
09	10	11
12	13	14
15	16	17

特别注意，和格式信息不同，版本信息在填充时需要反转，也即数据为从右到左填入。

输出最终矩阵

请注意，二维码规范要求二维码矩阵被一个静区包围：一个 4 模块宽的亮模块区域。