二维码学习笔记(番外) | 编码理论

二维码笔记系列：

• 『二维码学习笔记(一) | 二维码概述』
• 『二维码学习笔记(二) | 数据分析与数据编码』
• 『二维码学习笔记(三) | 纠错编码』
• 『二维码学习笔记(四) | 信息构建与模块放置』
• 『二维码学习笔记(五) | 数据掩码与版本信息』
• 『二维码学习笔记(六) | 二维码解码』

本篇是学习编码理论时写的杂记，未做整理，内容可能枯燥且冗余。

唠唠闲话

二维码是一种存储二进制数据的矩阵条码，其使用 RS(Reed-Solomon) 编码进行纠错。RS 码是一种线性码(Linear code)，其在现实生活中应用广泛，且存在高效的编解码算法。

本篇介绍编码原理，纠错算法以及拓展知识，跳转目录：

• 基础知识与纠错能力：
  • 分组码
  • 线性码
• 信息率
• 编码效率
• Reed Solomon 纠错

---

分组码

本节介绍分组码的定义例子，以及汉明距离等重要概念。

概述

在信息传输中，因传输通道噪音的干扰，接收端收到的信息与发送端发出的信息可能有误差。纠错码的引入，通过增加额外数据位，使传输的数据抵抗干扰的能力更加鲁棒(robust)。

在编码理论中，分组码(block code)是一大类重要的纠错码，它以块的形式对数据进行编码。分组码的抽象定义在概念上很有用，因为它允许编码理论家、数学家和计算机科学家以统一的方式研究所有分组码的局限性。这种局限性通常对编码界限进行研究，研究其与分组码不同参数的联系，例如信息率与检测纠正错误能力。

定义及例子

纠错码用于在受信道噪声影响的不可靠通信信道上可靠地传输数字数据。当发送者想要使用分组码传输长数据流时，发送者将流分成一些固定大小的片段，每个这样的片段称为消息(message)。分组码过程中，将每 message 单独编码成块(block)。然后，发送者将所有 block 传输给接收者，接收者又可以使用某种解码机制（希望）从可能损坏的接收 block 中恢复原始消息。整体传输的性能和成功取决于信道和分组码的参数。

1. 设 $\Sigma$ 为长度为 $q$ 的字符集，$\Sigma^n$ 为 n 元字符构成的集合

2. 将子集 $C\subseteq\Sigma^n$ 称为块长(block length)为 $n$ 的分组码

3. $C$ 的消息长度或维数定义为 $k=log_q(|C|)$

4. $C$ 的编码率或信息率(code rate/information rate) 定义为

   $$R=\frac{k}{n}=\frac{log_q(|C|)}{n}$$

   注：$R$ = 消息长度/编码块长度

5. $C$ 的元素 $x$ 称为码字(codeword)

6. 设分组码 $C$ 的距离为 $d$，将 $C$ 简称为 $(n, k, d)_{\Sigma}$ 分组码，距离定义在下边给出

7. 分组码可以理解为嵌入映射 $C\hookrightarrow\Sigma^n$，映射左侧为原始信息，右侧为加密后的信息

8. 例1：$\{hi,\ am,\ ok\}$ 为字符集 $\Sigma=\{a-z\}$ 的块长为 2 维数为 $log_{26}3$ 的分组码

9. 例2：$\{(1,1,1), (0,0,0)\}$ 为 $\Sigma=\{0,1\}$ 的块长 3 维数 1 的分组码，写成映射形式

   $$\begin{align*} \Sigma^1&\rightarrow\Sigma^3\\ 0&\rightarrow(0, 0, 0)\\ 1&\rightarrow(1, 1, 1) \end{align*}$$

10. 用大空间 $\Sigma^3$ 表示小空间 $\Sigma^1$ 的数据，能更好地处理错误信息：

• 检测错误(detect error)：假设传输 $(0,0,0)$ 时，发生了至多 2 个错误，比如

  $$(0,0,0)\rightarrow(0,1,1)$$

  接收端判断发现 $(0,1,1)\notin\Sigma^3$，立刻检测到错误
• 填补缺失(correct erasure)：假设传输 $(0,0,0)$ 时，丢失了至多 2 个位置的数据（丢失位置已知），比如

  $$(0,0,0)\rightarrow(*,0,*)$$

  接收端通过余下数据仍能还原初始数据
• 纠错能力(correct error)：假设传输 $(0,0,0)$ 时，有至多 1 个位置的数据错误，比如

  $$(0,0,0)\rightarrow(0,1,0)$$

  由于至多一个错误位置，初始数据只可能是 $(0,0,0)$

12. 显然，编码的纠错能力是有限的，假设数据 $(0,0,0)$ 传送时发生 2 个位置的错误，比如变成 $(0,1,1)$，接收端并不能确定原数据是 $(0,0,0)$ 还是 $(1,1,1)$。类似地，检测错误和填补缺失的能力也是有限的，假设传送时发生 3 个位置的错误，这种错误显然不能被检测出来。

汉明距离

下边引入距离定义，用来衡量处理错误的能力，不妨设字符集 $\Sigma$ 包含数字 0

1. 设码字 $c=(c_1,\cdots,c_n)\in\Sigma^n$，定义权重(weight) $wt(c) = \#\{i|c_i\neq 0\}$ 为 $c$ 的非零成分的数目。

2. 对 $c,c'\in\Sigma^n$，定义 $c$ 和 $c'$ 的汉明距离(Hamming distance) 为

   $$\Delta(c,c') = \#\{i|c_i\neq c_i'\}$$

   注：容易验证 $\Sigma^n$ 关于 $\Delta$ 作成度量空间

3. 编码 $C$ 的（最小）距离定义为

   $$\delta(C) = \min\{\Delta(c,c')\ |\ c\neq c'\in C\}$$

   距离 $d=\delta(C)$ 描述了码字 $c$ 转变为另一码字 $c'$ 的最少修改数

4. （定理）容易证明，分组码 $(n,k,d)_{\Sigma}$ 的错误处理能力为：

   • 编码 $C$ 能检测至多 $e\leq d-1$ 个错误
   • 编码 $C$ 能填补至多 $e\leq d-1$ 个缺失
   • 编码 $C$ 能纠正至多 $e\leq \lfloor\frac{d-1}{2}\rfloor$ 个错误，即 $2e\leq d-1$

5. 从图像理解汉明距离，以码字为圆心，半径 $e\leq \lfloor\frac{d-1}{2}\rfloor$ 的“小球”互不相交
   

衡量指标

编码在设计上有几个重要目标，或者说衡量指标：

• 处理错误的能力，比如检测错误，纠正错误
• 尽量小的冗余信息(minimize overhead)
• 计算效率，比如编码，解码和纠错等操作的执行效率

在分组码 $(n,k,d)_{\Sigma}$ 中，错误处理能力用距离 $d$ 或相对距离 $d'$ 描述，冗余信息用编码率/信息率 $R$ 表述。

一般地，编码距离 $d$ 越大，错误处理能力越强，但相应地，冗余信息将越多，这导致了信息率 $R$ 的减小。因此，协调错误处理能力 $d$ 与信息率 $R$ 是编码领域的重要问题，然而，如何制定最佳权衡策略(best trade-off)还是个开问题。

尽管如此，有不少研究在某些方面给出了解答，例如下边要介绍的汉明界。

有时也用相对距离 $d'=\frac{d}{n}$ 来衡量编码的纠错能力。

汉明界

在编码理论领域，汉明界(Hamming Bound) 是对分组码参数的限制，它对编码空间的利用率提出了重要限制。汉明界也被称为球包装界或体积界，这可以从推导过程看出来。

1. 设 $x\in\Sigma^n$，如下定义 $B_{\Sigma^n}(x, e)$ ，并称为 $x$ 的以 $e$ 为半径的 Hamming Ball。

   $$B_{\Sigma^n}(x, e) = \{y\in\Sigma^n\ |\ \Delta(x,y)\leq e\}$$

2. 将汉明球 $B_{\Sigma^n}(x, e)$ 包含的 $\Sigma^n$ 元素个数称为球的体积(Volume) ，记为

   $$Vol_q(e,n)=|B_{\Sigma^n}(x, e)|,\ where\ q=|\Sigma|$$

   由于对称性，球体积与 $x$ 的选取无关，因而体积定义中不含参数 $x$

3. 推导易得下边公式

   $$Vol_q(e,n) = \sum_{i=0}^e\begin{pmatrix}n\\ i\end{pmatrix}(q-1)^i$$

   其中加项 $\begin{pmatrix}n\\ i\end{pmatrix}(q-1)^i$ 代表与 $x$ 的汉明距离为 $i$ 的 $\Sigma^n$ 中的元素数目。换言之，这些元素可通过 $x$ 修改 i 个位置数据得到。

4. 设 $d$ 为 $C$ 的距离，同前边示意图易知，汉明球 $B_{\Sigma^n}(x,\lfloor\frac{d-1}{2}\rfloor),x\in C$ 之间两两不交，继而有

   $$|C|\cdot Vol_q(\lfloor\frac{d-1}{2}\rfloor,n) \leq |\Sigma^n| \leq q^n$$

   取等当且仅当这些汉明球覆盖了整个空间；整理可得

   $$\begin{align*} &\log_q(|C|) + \log_q(Vol_q(\lfloor\frac{d-1}{2}\rfloor,n))\leq n\\ \Rightarrow &\ k+\log_q(Vol_q(\lfloor\frac{d-1}{2}\rfloor,n))\leq n\\ \Rightarrow &\ \frac{k}{n}+\frac{\log_q(Vol_q(\lfloor\frac{d-1}{2}\rfloor,n))}{n}\leq 1\\ \Rightarrow &\ R \leq 1-\frac{\log_q(Vol_q(\lfloor\frac{d-1}{2}\rfloor,n))}{n} \end{align*}$$

   上式表明，当编码块长 $n$，字符集长 $q$ 以及编码距离 $d$ 确定时，信息率 $R$ 存在不等式右侧给出的上界，这一上界便称为汉明界

5. 汉明界在某些角度上回答了编码距离与信息率的关系，假设编码块长 $n$ 和字符集 $\Sigma$ 确定，汉明界表明：当编码距离 $d$ 确定时，信息率 $R$ 不会超过某个数值。而取到边界当且仅当所构造编码的半径为 $\lfloor\frac{d-1}{2}\rfloor$ 的汉明球覆盖了整个空间。达到汉明界的编码被称为完美编码(perfect code) 或汉明码(Hamming code)

6. 举个例子，考虑二进制字符集 $\Sigma=\{0,1\}$，设编码的块长为 $n=7$，距离为 $d=3$，维数为 $k$，计算汉明界

   $$\begin{align*} R = \frac{k}{n}&\leq 1-\frac{\log_q(Vol_q(\lfloor\frac{d-1}{2}\rfloor,n))}{n}\\ &= 1-\frac{\log_2(Vol_2(1,7))}{7},\ Vol_2(1,7) = 1+7\\ &= 1-\frac{\log_2(8)}{7} = \frac{4}{7} \end{align*}$$

   根据汉明界，编码维数 $k\leq 4$，如下编码可以取到等号

   $$\begin{align*} C:\Sigma^4&\rightarrow \Sigma^7\\ \begin{pmatrix}x_1\\ x_2\\ x_3\\ x_4\end{pmatrix}& \mapsto\begin{pmatrix} 1& & & \\ & 1& & \\ & &1 & \\ & & &1 \\ 0& 1& 1 &1 \\ 1& 0 &1 &1 \\ 1& 1 & 0 &1 \\ \end{pmatrix} \begin{pmatrix}x_1\\ x_2\\ x_3\\ x_4\end{pmatrix} = \begin{pmatrix}x_1\\ x_2\\ x_3\\ x_4\\ x_2+x_3+x_4 \\ x_1+x_3+x_4 \\ x_1+x_2+x_4\end{pmatrix} \end{align*}$$

例中，编码用线性变换定义，这种编码方式称为线性码，Reed Solomon 编码便是一类特殊的线性码。

---

线性码

线性码是一种纠错码，任何码字的线性组合也是一个码字。线性码传统上分为分组码和卷积码，以下仅讨论分组码。

下设 $\mathbb{F} = \mathbb{F}_q$ 为 $q$ 个元素构成的有限域。

基本概念

1. （定义） 编码空间 $\mathbb{F}^n$ 的真子空间 $C=\mathbb{F}^k$ 称为 $\mathbb{F}$ 上的维数为 $k$，块长为 $n$ 的线性码(Linear Code)。将矩阵 $G\in\mathbb{F}^{n\times k}$ 称为 $C$ 的生成元矩阵(Generator Matrix)，若

   $$C=column\ span(G)=\{G\cdot x\ |\ x\in\mathbb{F}^k\}$$

   借助生成矩阵 $G$，线性码 $C$ 可写为映射形式

   $$\begin{align*} C:\mathbb{F}^k&\rightarrow\mathbb{F}^n\\ X&\mapsto GX,\ where\ X=\begin{pmatrix} x_1\\ x_2\\\vdots\\ x_k \end{pmatrix} \end{align*}$$

2. 生成元矩阵不唯一：任意可逆矩阵左乘生成元矩阵，仍得到生成元矩阵。特别地，通过调整 $\mathbb{F}^n$ 的索引，总能左乘得到上分块为单位阵的生成元矩阵：

   $$\begin{align*} C:\mathbb{F}^k&\rightarrow\mathbb{F}^n\\ X &\mapsto \begin{pmatrix}I\\ G'\end{pmatrix} X=\begin{pmatrix} X\\G'X \end{pmatrix} \end{align*}$$

   容易发现，初始信息 $X$ 嵌在编码后的信息中。我们将满足这一性质的编码称为系统码(Systematic Code)

3. 称 $H\in\mathbb{F}^{(n-k)\times n}$ 为线性码 $C$ 的奇偶检验矩阵(Parity Check Matrix)，若

   $$\begin{align*} \ker(H) &= \{x\in\mathbb{F}^n|Hx=0\}\\ &= \{Gy\in\mathbb{F}^n| y\in\mathbb{F}^k\}=im(G) \end{align*}$$

   由线性代数知识，易见 $rank(H)=n-k, rank(G)=k$，即矩阵 $G$ 为列满秩，矩阵$H$ 为行满秩

4. 设 $(C,G,H)$ 为一组线性码，则 $(C^\perp, H^t, G^t)$ 也为一组线性码，称为 $C$ 的对偶码(Dual Code)，其中

   $$C^{\perp} = \{x\in\mathbb{F}^n|\lang x,y\rang=x^ty=0,\forall\ y\in C\}$$

注：编码可以理解为信息空间到表示空间的单射，线性码则是通过列满秩矩阵给出这个单射。

编码距离

相比分组码，线性码的编码距离可以用矩阵 $G$ 或 $H$ 计算。

1. 以下命题等价

   1. 编码 $C$ 的汉明距离为 $d$
   2. $G$ 列空间非零向量最小权重，即

      $$\min\{wt(x) | x\in column\ span\ of(G)\}$$

   3. $H$ 的任意 $d-1$ 个列向量线性无关，且存在长为 $d$ 的线性相关列向量组；换言之，$H$ 的线性相关列向量组的最小长度为 $d$
   4. $G$ 的任意 $n-d+1$ 个行向量构成的向量组中，存在 $k$ 个线性无关向量；换言之，$G$ 的任意 $n-d+1$ 行构成的矩阵列满秩

2. 我们依次证明这几个命题

   • $(1)\Leftrightarrow (2)$
     根据线性性：

   $$d=\delta(c,c')=\delta(c-c', 0) = wt(c-c')=wt(c''),c''\in C$$

   • $(2)\Leftrightarrow(3)$
     先将 $H$ 列分块化，并由 $\ker(H)=C$ 知

     $$\begin{align*} H = \begin{pmatrix} H_1&\cdots&H_n \end{pmatrix}\\ x=(x_1,\cdots,x_n)^t\in C &\Leftrightarrow Hx = O\\ &\Leftrightarrow \sum_{i=1}^nx_iH_i=O \end{align*}$$

   $x\in C$ 的 $r$ 个非零元数目对应得到 $H$ 中 $r$ 个线性相关的列向量

   • $(1)\Leftrightarrow(4)$
     根据定义：$C$ 的编码距离为 $d$ 等价于 $\forall y\in C$，$y$ 的任意 $d-1$ 项出错不会得到另一个码字；等价于方程组 $Gx=y$ 中，将 $G,y$ 的任意 $d-1$ 个行向量丢弃得到的方程 $G'x=y'$，其只有唯一解 $x$；等价于 $G$ 去掉任意 $d-1$ 行，得到的矩阵列满秩

3. 一般地，选取列向量 $x\in C$ 得距离上界 $d\leq wt(x)$，选取 $H$ 的 $r$ 个线性相关向量得到距离下界 $d\geq r$，比如前边例子

   $$G = \begin{pmatrix} 1& & & \\ & 1& & \\ & &1 & \\ & & &1 \\ 0& 1& 1 &1 \\ 1& 0 &1 &1 \\ 1& 1 & 0 &1 \\ \end{pmatrix},H=\begin{pmatrix} 0&1&1&1&1&0&0\\ 1&0&1&1&0&1&0\\ 1&1&0&1&0&0&1 \end{pmatrix}$$

   由 $G$ 的第一列非零数得 $d\leq 3$，由 $H$ 前三列向量线性相关性 $d\geq 3$，于是 $d=3$

---

信息率

前边提到衡量编码的三个重要指标：处理错误能力，尽量小的冗余信息，以及计算效率。关于错误处理能力，我们用编码距离 $d$ 来衡量，对于线性码还可以借助生成元矩阵 $G$ 和奇偶检验矩阵 $H$ 做相关计算；对于冗余信息，Hamming Bound 给出了某些方面的回答，本节将对信息率的边界做更深入的探讨。

本节侧重介绍辛格尔顿界，其与 Reed Solomon 纠错直接关联，其他作为拓展兴趣只做科普性地介绍，不讨论证明。

辛格尔顿界

在编码理论中，辛格尔顿界(Singleton Bound) 以 Richard Collom Singleton 命名，其表明 $(n,k,d)_q$ 分组码中，信息长满足 $k\leq n-d+1$，继而

$$R\leq 1-\frac{d-1}{n}$$

这个定理的证明非常简单，考虑复合映射 $\varphi$ 为单射

$$\begin{align*} \varphi:\Sigma^k&\rightarrow\Sigma^n\rightarrow\Sigma^{n-d+1}\\ c&\mapsto(c_1,\cdots, c_{n})\mapsto(c_{d},\cdots,c_n) \end{align*}$$

$\varphi$ 必为单射，由于 $c$ 与 $c'$ 至多前 d-1 个位置不同，即

$$\begin{align*} \varphi(c)=\varphi(c')&\Rightarrow(c_{d},\cdots,c_n)=(c_{d}',\cdots,c_n')\\ &\Rightarrow \Delta(c,c')\leq d-1\\ &\Rightarrow c=c' \end{align*}$$

由 $\varphi$ 为单射，比较集合立得 $k\leq n-d+1$。

对于线性码，从上一节编码距离的刻画(4) 立知，$n-d+1\geq k$。

GV 界

在编码理论中，GV Bound(Gilbert–Varshamov Bound) 是由 Edgar Gilbert 和 Rom Varshamov 分别独立提出的，关于编码（未必线性）参数的边界，Varshamov 通过使用线性码的概率方法证明了这一界限。有关该证明的更多信息请参阅这里。

定理 (Gilbert–Varshamov) 设 $q$ 为素数幂次，$d\leq n$，则存在线性码 $C$ 使得

• $C$ 的块长为 $n$，字符集数目为 $q$， 汉明边界为 $d$
• $C$ 的信息率 $R=\frac{k}{n}$ 满足下边性质

$$\begin{align*} R\geq 1- \frac{log_q(Vol_q(d-1, n))-1}{n} \end{align*}$$

定理证明过程并不复杂，但使用了分析概率的方法，属于非构造性证明，感性趣看这个视频。

渐进分析(Asymptotics)

GV Bound 给出了 $R$ 的下界，结合 Hamming Bound 得到

$$1- \frac{log_q(Vol_q(d-1, n))-1}{n} \leq \ R \leq 1-\frac{\log_q(Vol_q(\lfloor\frac{d-1}{2}\rfloor,n))}{n}$$

这个不等式中，信息率 $R$ 与参数 $d,n,q$ 均有关，且形式复杂，不利于理解 $R$ 的性质。为此，我们使用渐进分析的方式，通过取极限去除某些参数，以研究 $R$ 最本质的性质。

信息率与距离

1. 设 $\mathfrak{C}=\{C_i\}_{i=1}^\infin$ 为编码构成的序列，其中 $C_i$ 为 $(n_i,k_i,d_i)_{q_i}$ 分组码，定义序列 $\mathfrak{C}$ 的信息率为

   $$R(\mathfrak{C}) :=\lim_{i\rightarrow\infty}\frac{k_i}{n_i}$$

   定义 $\mathfrak{C}$ 的相对距离(简称距离) $\delta(C)$ 为

   $$\delta(\mathfrak{C}) :=\lim_{i\rightarrow\infty}\frac{d_i}{n_i}$$

2. 前边讨论汉明界时，举了 $(7,4,3)_2$-汉明码的例子，类似地，容易构造编码序列 $\mathfrak{C}=\{C_i\}_{i=1}^\infty$，其中 $C_i$ 为 $(2^i-1, 2^i-i-1, 3)_2$ 汉明码，此时

   $$\begin{align*} R(\mathfrak{C}) &= \lim_{i\rightarrow\infty}\frac{2^i-i-1}{2^i-1}=1\\ \delta(\mathfrak{C}) &=\lim_{i\rightarrow\infty}\frac{3}{n_i}=0 \end{align*}$$

   $C$ 的信息率趋近于 $1$，但距离趋近于 0，即纠错能力趋于没有。

3. 我们希望在 $\delta(\mathfrak{C})$ 和 $R(\mathfrak{C})$ 中找到最佳的协调方式，特别地，将满足 $\delta(\mathfrak{C})\neq 0\neq R(\mathfrak{C})$ 的编码序列称为渐进好的(Asymptotically Good)

边界分析

1. GV Bound 和 Hamming Bound 公式中的体积球 $Vol$ 不利于讨论，为此先定义 q-ary 熵函数(q-ary entropy function)，用于化简公式

   $$\begin{align*} H_q:[0,1]&\rightarrow[0,1]\\ x&\mapsto xlog_q(q-1)-xlog_q(x)-(1-x)log_q(1-x) \end{align*}$$

   • 当 $x\rightarrow 0$ 时，上式趋 0
   • 当 $x\rightarrow 1$ 时，上式趋 $log_q(q-1)$
   • 当 $q\rightarrow \infty$ 时，$H_q(x)\rightarrow x$
   • 图像整体开口朝下

2. 设 $q\geq 2 \in\mathbb{Z},\ 0\leq p\leq 1-\frac{1}{q}$，则（略去证明）

   $$\begin{align*} q^{n\cdot H_q(p)-o(n)}\leq Vol_q(pn, n)\leq q^{n\cdot H_q(p)} \end{align*}$$

3. 根据 Hamming Bound，对任意编码序列 $\mathfrak{C}$，有

   $$\begin{align*} R &\leq 1-\frac{1}{n}\log_q(Vol_q(\lfloor\frac{d-1}{2}\rfloor,n))\\ &\underset{n\rightarrow \infty}{\leq}1-H_q(\frac{\delta(\mathfrak{C})}2) \end{align*}$$

   根据 GV Bound，存在编码序列 $\mathfrak{C}$，使得

   $$\begin{align*} R&\geq 1- \frac{1}{n}(log_q(Vol_q(d-1, n))-1)\\ &\geq 1-\frac{1}{n}(n\cdot H_q(\frac{d-1}{n})-o(n)-1)\\ &\underset{n\rightarrow \infty}{\geq}1-H_q(\delta(\mathfrak{C}))\\ \end{align*}$$

4. 综上，有

   $$1-H_q(\delta(\mathfrak{C}))\leq R(\mathfrak{C})\leq 1-H_q(\frac{\delta(\mathfrak{C})}2)$$

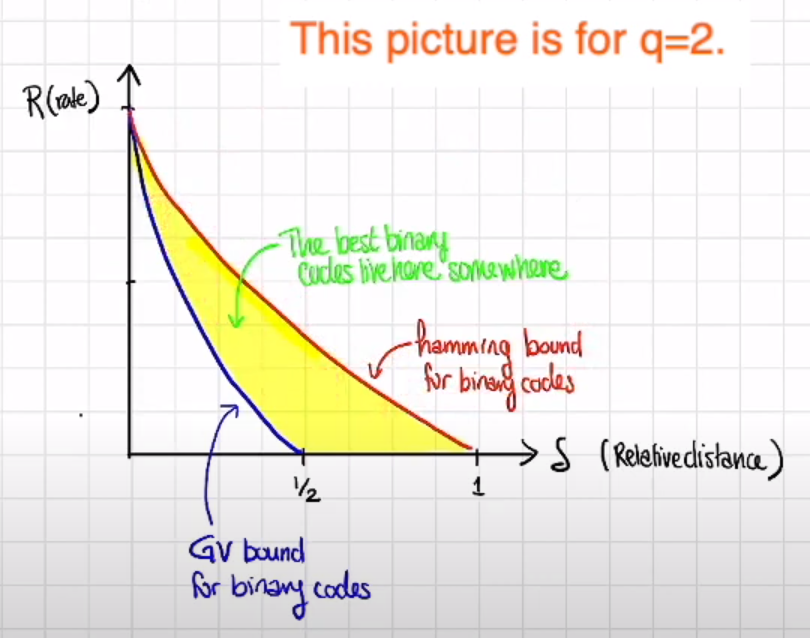
   我们将这两个边界分别称为编码序列 $\mathfrak{C}$ 的渐进 GV Bound 和渐进 Hamming Bound。当 $q=2$ 时，图像表现为
   

5. 延伸

   • Q1：是否存在编码序列，满足渐进 GV Bound，即落在黄色区域
     • 当 $q\geq 49$ 时，问题成立
     • 当 $q=2$ 时，这还是个开问题
   • 能否构造编码序列，满足渐进 GV Bound，同样地，这个问题也仅在 $q$ 足够大时存在
   • 渐进 GV Bound 给出蓝线以下的存在性，继而说明了存在“渐近好的”编码序列
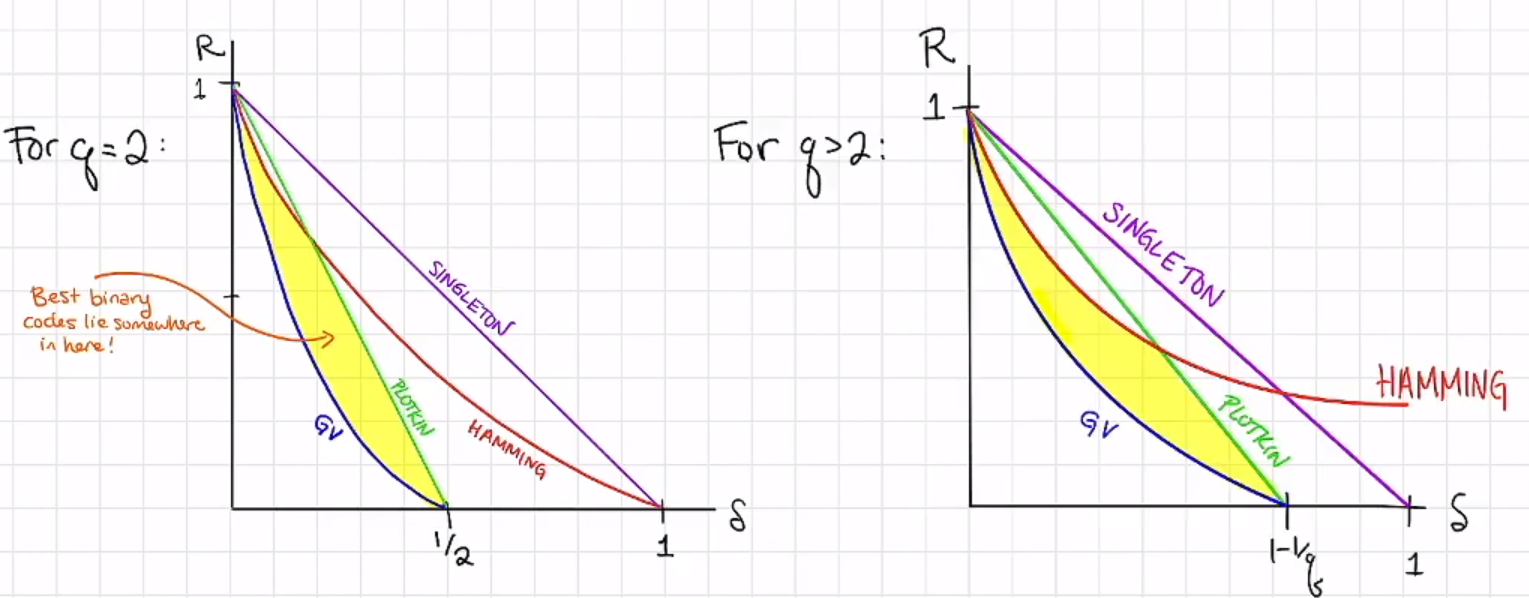
   • 关于边界分析，还有 Plotkin Bound 等，将图像进一步细化，这些都描述了比率 $R(\mathfrak{C})$ 与距离 $\delta(\mathfrak{C})$ 之间的关系
     
   • 特别注意，本节讨论对编码序列的渐进分析，从图像上看 Singleton Bound 始终在 Plotkin Bound 上方，但这是在 $q$ 固定下取极限得到的图像；落实到具体编码时，Singleton Bound 是可以取到的，比如 RS 码。

---

编码效率

概述

本节讨论编码效率问题，特别地，博客只讨论线性分组码的情形。

编码过程的这几个步骤涉及计算：

• 信息编码，即 $\mathbb{F}_q^k\rightarrow\mathbb{F}_q^n$
• 信息解码，即 $Im(C)\rightarrow\mathbb{F}_q^k$
• 填补缺失，比如 $(*,0,0) \rightarrow (0,0,0)$
• 检测错误，比如 $(1,1,0)$
• 计算编码距离
• 纠正错误，比如 $(1,0,0)\rightarrow(0,0,0)$

前四步存在高效算法(多项式时间)，但计算编码距离和纠错不存在处理一般情形的高效算法。

这种纠错上的困难性，既是坏处也是好处：

• 坏处在于：我们不能用任意线性码来制定编码规则，否则纠错带来的时间开销过大，效率过低
• 好处在于，这种困难性可以应用于非对称加密系统

坏处是可以避免的，比如构造特殊编码，使编码具备更多性质，允许更多操作，继而存在更高效的算法，应用上我们并不需要设计能处理一般编码的算法。

好处是这类数论难题通常导致加密算法的产生，这部分理论与二维码关联很低，放在公钥系统中单独介绍。

编码算法

下边介绍线性码中编码，解码，补缺，检错，求距离以及纠错这些步骤的一般计算方法。

下设 $C$ 为 $(n, k,d)_q$ 线性分组码，生成元矩阵为 $G\in \mathbb{F}^{n\times k}$，奇偶检验矩阵为 $H\in \mathbb{F}^{k\times n}$，设 $x=(x_1,\cdots,x_k)^t\in C$ 为信息。

1. 编码：用矩阵 $G$ 左乘信息 $x$

   $$\begin{align*} C:\mathbb{F}_q^k&\rightarrow\mathbb{F}_q^n\\ x&\mapsto Gx=x' \end{align*}$$

2. 解码：由线性代数知识易得矩阵 $G'\in \mathbb{F}^{k\times n}$ 使得 $G'G$ 为 $k$ 阶单位矩阵。左乘矩阵 $G'$ 即从 $x'$ 中解码信息 $x$。

3. 检错：根据 $\ker(H)=Im(C)$，只需判断 $Hx'$ 是否为 0。

4. 补缺：不妨设 $x'$ 缺失了前 $e<d$ 个数据，将 $G$ 相应分块化，得

   $$\begin{align*} Gx =\begin{pmatrix} G_0 \\ G_1 \end{pmatrix} x=\begin{pmatrix} x_1'\\\vdots\\ x_{e-1}'\\ x_e'\\ \vdots\\ x_n' \end{pmatrix}=\begin{pmatrix} *\\\vdots\\ *\\ x_e'\\ \vdots\\ x_n' \end{pmatrix} \end{align*}$$

   反解得到原始数据 $x$

   $$\begin{align*} G_1x=\begin{pmatrix} x_e'\\ \vdots\\ x_n' \end{pmatrix}, x=G_1^{-1}\begin{pmatrix} x_e'\\ \vdots\\ x_n' \end{pmatrix} \end{align*}$$

   当 $e<d$ 时，左侧方程组必有解，而 RS 码中 $G_1$ 还是可逆的，此时直接左成逆矩阵还原数据。

5. 求距离：回顾介绍了编码距离 $d$ 的两个计算性质：

   • $d$ 为生成元矩阵 $G$ 列空间中非零向量的最小权
   • $d$ 为奇偶检验矩阵 $H$ 的线性相关列向量组的最小长度

   这两条性质给出了 $d$ 的上下界，因此随机选取列向量来计算 $d$，但文献论证了计算一般线性码的编码距离不是 RP 问题(nondeterministic polynomial time)，也即不存在针对一般线性码的高效算法

6. 纠错：假设码字 $x'=Gx+z$，其中 $z$ 为纠错范围内的错误扰动，左乘矩阵 $H$ 得

   $$b = Hx' = H(Gx+z) = HGx + Hz = Hz$$

   求解线性方程组 $Hz=b$ 计算错误扰动 $z$，由于 $z$ 处在纠错范围内，存在唯一向量 $z$ 使得

   $$Hz=b,\ wt(z) \leq \lfloor\frac{d-1}{2}\rfloor$$

   线性方程组的解构成了一个仿射空间(线性空间+平移向量)，问题等同于求该空间中权重最小的向量。然而这个问题的求解仍是困难的，哪怕对 RS 码，参阅文献：Maximum-Likelihood Decoding of Reed-Solomon Codes is NP-hard

注：表面上看，纠错只是解线性方程，但由于这是对有限域上讨论，且问题不是求出方程的一个解，而是计算最小解。由于解空间是随着维数以指数形式增长，暴力破解自然行不通。这种表明简单，但应用到有限域就变得复杂的现象在数论中经常出现，比如计算离散对数 $log_q(a)$ 。

---

最后，回到文章重点，RS 码及纠错算法，由于 RS 码取到了 Singleton Bound，编码距离计算简单，难点在纠错上。

Reed-Solomon 纠错

Reed-Solomon 码是一组纠错码，由 Irving S. Reed 和Gustave Solomon 在 1960 年引入。它有许多应用，比如 MiniDiscs、CD、DVD、蓝光光盘、二维码、DSL、WiMAX 等等。

RS 码具有以下特点：

• RS 码满足 Singleton Bound
• RS 码存在高效的解码算法
• RS 码在现实生活中被广泛应用

背景知识

具备高效算法的编码通常具有丰富的结构性质，RS 码便是如此，其为一类特殊线性码，以范德蒙德矩阵(Vandermonde matrix) 为生成元矩阵。

我们先介绍理论基础，再给出 RS 码的定义和性质（这么安排并不好，有空调整一下）。

下设 $\mathbb{F}$ 为数域，$\alpha=(\alpha_0,\cdots,\alpha_{n-1})\in\mathbb{F}^{n-1}$，且 $\alpha_i$ 互不相等。

1. 数域可以分两大类，有理数域 $\mathbb{Q}$，实数域 $\mathbb{R}$ 和复数域 $\mathbb{C}$ 等属于特征 0 域；有限域 $F_p$ 及其扩张，属于特征 p 域，线性代数理论对两类数域均适用。

2. 称数域 $\mathbb{F}$ 为有限域，若其仅有有限个元素，并将包含 $q$ 个元素的有限域记为 $\mathbb{F}_q$，有限域也被称为伽罗瓦域(Galois Filed)。由近世代数可知

   • 有限域均形如 $\mathbb{F}_q$，其中 $q=p^r$， $p$ 为素数
   • 同阶的有限域相互同构
   • 记 $\mathbb{F}_q^*=\mathbb{F}_q-\{0\}$，其乘法结构作成 $q-1$ 阶循环群
   • 特别地，$r$ 取 1 时，$\mathbb{F}_p$ 称为素域，其结构简单，同构于 $\mathbb{Z}/p\mathbb{Z}$
   • 一般地，$\mathbb{F}_q$ 同构于素域 $\mathbb{F}_p$ 关于 $x^r-1$ 的分裂域。当 $r\neq 1$时， $\mathbb{F}$ 结构复杂，而不是简单的模 $q$ 结构。

3. 性质：$\mathbb{F}$ 上的 $n$ 次多项式 $f(x)$ 至多存在 $n$ 个根。若干说明：

   • “$n$ 个根”指 $\mathbb{F}$ 上的根，通过带余除法和归纳法容易证明
   • 代数基本定理表明 $n$ 次多项式恰有 $n$ 个根，这里 $n$ 个根指代数闭包 $\bar{\mathbb{F}}$ 上的根，比如实数域上 $x^2+1=0$ 没有根，但在代数闭域 $\mathbb{C}$ 上有两个根
   • 零多项式的次数一般假定为无穷

4. 如下定义范德蒙德矩阵 $V(\alpha,k)\in\mathbb{F}^{n\times k}$

   $$V(\alpha,k)= \begin{pmatrix} 1 & \alpha_0 & \alpha_0^2 & \cdots & \alpha_0^{k-1}\\ 1 & \alpha_1 & \alpha_1^2 & \cdots & \alpha_1^{k-1}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \alpha_{n-1} & \alpha_{n-1}^2 & \cdots & \alpha_{n-1}^{k-1} \end{pmatrix}$$

   当 $k\leq n$ 时，由范德蒙德行列式易证 $V(\alpha,k)$ 的秩为 $k$

   $$\begin{align*} \begin{vmatrix} 1 & \alpha_0 & \alpha_0^2 & \cdots & \alpha_0^{k-1}\\ 1 & \alpha_1 & \alpha_1^2 & \cdots & \alpha_1^{k-1}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \alpha_{k-1} & \alpha_{k-1}^2 & \cdots & \alpha_{k-1}^{k-1} \end{vmatrix}=\prod_{i>j}(\alpha_i-\alpha_j)\neq 0 \end{align*}$$

5. 范德蒙德矩阵与多项式有紧密联系：左乘运算可转化为多项式运算

   $$\begin{align*} \begin{pmatrix} 1 & \alpha_0 & \alpha_0^2 & \cdots & \alpha_0^{k-1}\\ 1 & \alpha_1 & \alpha_1^2 & \cdots & \alpha_1^{k-1}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \alpha_{n-1} & \alpha_{n-1}^2 & \cdots & \alpha_{n-1}^{k-1} \end{pmatrix} \begin{pmatrix} a_0\\ a_1\\ \vdots\\ a_{k-1} \end{pmatrix}= \begin{pmatrix} \sum\limits_{i=0}^{k-1}a_i\alpha_0^i\\ \sum\limits_{i=0}^{k-1}a_i\alpha_1^i\\ \vdots\\ \sum\limits_{i=0}^{k-1}a_i\alpha_{n-1}^i \end{pmatrix}= \begin{pmatrix} f(\alpha_0)\\ f(\alpha_1) \\ \vdots \\ f(\alpha_{n-1}) \end{pmatrix} \end{align*}$$

   其中 $f(x)=\sum\limits_{i=0}^{k-1}a_ix^i$，从这一性质也能看出 $V(\alpha,k)$ 为列满秩矩阵

   $$\begin{align*} V(\alpha,k)X=O&\Leftrightarrow f(\alpha_i)=0,\ \forall\ 0\leq i\leq n\\ &\Rightarrow f=0\quad (\deg(f)<=n)\\ &\Rightarrow X=(a_0,\cdots, a_k)^t=O \end{align*}$$

   特别地，当 $k=n$ 时，$V(\alpha,k)$ 为可逆矩阵

6. 推论：对任意 $\{y_i\}_{i=0}^{k-1}\subseteq\mathbb{F}_q^n$，存在唯一次数不大于 $k-1$ 的多项式 $f$，使得 $f(\alpha_i)=y_i$。具体地，$f$ 的各项系数$\{a_i\}_{i=0}^{k-1}$ 由以下线性方程组得到

   $$V(\alpha,n) \begin{pmatrix} a_0\\ a_1\\ \vdots \\ a_{k-1} \end{pmatrix}= \begin{pmatrix} y_0\\ y_1\\ \vdots \\ y_{n-1} \end{pmatrix}$$

7. 推论2：有限域上，任意映射 $\mathbb{F}_q\rightarrow\mathbb{F}$ 可写为次数不超过 $q-1$ 的多项式。此外，利用性质 $x^q=x$，任意多项式可以转化为次数不超过 $q-1$ 的多项式。

这个现象很有趣：有限域上的函数没有可积可微的概念，所有映射都是多项式！且函数集是有限集。

基本概念

Reed Solomon 码是满足 Singleton Bound 且具有高效算法的一类编码。（以下是 RS 码的 Original View）

下设 $q\geq n\geq k$，$\alpha=(\alpha_0,\cdots,\alpha_{n-1})\in\mathbb{F}_q^n$ 且其中元素互不相同。

1. 如下定义 $\mathbb{F}_q^n$ 的子集 $RS_q(\alpha,n,k)$，称为信息长 $k$，块长 $n$ 的关于向量 $\alpha$ 的 Reed-Solomon 码

   $$RS_q(\alpha,n,k)=\{(f(\alpha_0), \cdots, f(\alpha_{n-1}))|f(x)\in\mathbb{F}_q[x],\ \deg(f)\leq k-1\}$$

2. 写成线性变换形式

   $$\begin{align*} RS_q(\alpha,n,k):\mathbb{F}_q^k&\hookrightarrow \mathbb{F}_q[x]&\rightarrow \mathbb{F}_q^n\qquad\qquad\\ \begin{pmatrix}a_0\\\vdots\\a_{n-1}\end{pmatrix} &\mapsto f(x)=\sum_{i=0}^{k-1}a_ix^i &\mapsto \begin{pmatrix}f(\alpha_0)\\\vdots\\ f(\alpha_{n-1})\end{pmatrix} \end{align*}$$

   根据上一节讨论，其生成元矩阵为 $V(\alpha, k)$

3. RS 码满足 Singleton Bound，根据以下等价关系可证

   • $d$ 为 $RS_q(\alpha,k,n)$ 的编码距离
   • $d$ 为生成元矩阵 $V(\alpha,k)$ 列空间的最小权重
   • $d$ 为 n - ($V(\alpha,k)$ 列空间的最大零数)

   一方面，由于 $\deg(f)\leq k-1$， $f(\alpha_i)$ 中至多有 $k-1$ 项为 0，因而 $d\geq n-(k-1)$；另一方面，取 $f(x)=(x-\alpha_0)\cdots(x-\alpha_{k-1})$ 得到权重为 $n-k+1$ 的列向量，证毕。

4. 将满足 Singleton Bound 的编码称为 MDS(Maximum Distance Separable) 码 。容易证明：$(n,k,d)_q$ 线性分组码为 $MDS$ 码当且仅当其生成元矩阵 $G$ 的任意 $k\times k$ 阶子矩阵可逆。

特殊 RS 码

我们考虑在编码中更常用一种的 RS 码：取 $n=q-1$。

1. 我们先给出一个引理，用于求解该 RS 码的奇偶检验矩阵

   $$\begin{align*} \sum_{a\in\mathbb{F}_q}a^d=0,\ \forall\ 0<d<q-1 \end{align*}$$

   证明：设 $\gamma$ 为 $\mathbb{F}_q^*$ 乘法群的生成元

   $$\begin{align*} \sum_{a\in\mathbb{F}_q}a^d &=\sum_{a\in\mathbb{F}^*}a^d =\sum_{i=1}^{q-1}\gamma^{i\cdot d}\\ &=\sum_{i=1}^{q-1}(\gamma^{d})^i =\frac{1-(\gamma^d)^q}{1-\gamma^d}-1=0 \end{align*}$$

   根据循环群性质， $a^{q-1}\equiv 1,\forall a\neq 0$，继而有 $(\gamma^d)^q\equiv \gamma^d$

2. 设 $\alpha=(\gamma^1,\gamma^2\cdots,\gamma^{p-1})$，$RS_q(\alpha,k,n)$ 的生成元矩阵 $V(\alpha,k)$ 为

   $$\begin{align*} V(\alpha,k)&=\begin{pmatrix} 1 & \gamma^1 & \gamma^2 & \cdots & \gamma^{k-1}\\ 1 & (\gamma^2)^1 & (\gamma^2)^2 & \cdots & (\gamma^2)^{k-1}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & (\gamma^{p-2})^1 & (\gamma^{p-2})^2 & \cdots & (\gamma^{p-2})^{k-1}\\ 1 & 1 & 1 & \cdots & 1 \end{pmatrix} \end{align*}$$

   其奇偶检验矩阵由下式确定

   $$\begin{align*} RS_q(\alpha,n,k)&=\{(c_1,c_2,\cdots,c_{q-1})|c(\gamma^j)=0,\forall 1\leq j\leq n-k\}\\ where\ c(x)&=\sum\limits_{l=1}^{q-1}c_lx^l =\sum\limits_{l=1}^{q-1}f(\gamma^l)x^l\\ \end{align*}$$

   利用前一引理易证

   $$\begin{align*} c(\gamma^j) &= \sum_{l=1}^{p-1}f(\gamma^l)\cdot(\gamma^j)^l\\ &=\sum_{l=1}^{p-1}\left(\sum_{i=0}^{k-1}a_i(\gamma^l)^i\right)\cdot(\gamma^j)^l\\ &=\sum_{i=0}^{k-1}a_i\left(\sum_{l=1}^{p-1}(\gamma^l)^{(i+j)}\right) =0 \end{align*}$$

   最后一式，$1\leq i+j\leq n-k+i\leq n-1\leq q-1$
   $c(\gamma^j)=0$ 的必要性通过比较维数立证。

3. 推论：$RS_q((\gamma^1,\cdots,\gamma^{q-1}),n,k)$ 的奇偶检验矩阵为

   $$\begin{align*} H &=V((\gamma^1,\cdots,\gamma^{q-1}),n-k)^t\\ &=\begin{pmatrix} 1&\gamma&\gamma^2&\cdots&\gamma^{n-1}\\ 1&(\gamma^2)^1&(\gamma^2)^2&\cdots&(\gamma^2)^{n-1}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 1&(\gamma^{n-k})^1&(\gamma^{n-k})^2&\cdots&(\gamma^{n-k})^{n-1}\\ \end{pmatrix} \end{align*}$$

4. 推广的RS码(Generalized RS code) 定义如下

   $$GRS_q(\alpha,n,k;\overrightarrow\lambda)= \{(\lambda_0f(\alpha_0),\lambda_1f(\alpha_1),\cdots,\lambda_{n-1}f(\alpha_{n-1})),f\in\mathbb{F}_q[x],\deg(f)\leq k-1\}$$

   其中 $\alpha\in(\mathbb{F}_q^*)^n$ ，此外生成元矩阵为

   $$\begin{align*} G &=M\cdot V(\alpha,k),\ diag(M)=(\lambda_0,\cdots,\lambda_{n-1}) \end{align*}$$

   一般地，可以推导 $GRS_q(\alpha,n,k;\overrightarrow\lambda)$ 的对偶码

简单说，RS 码为多项式 $f$ 到 $f.\alpha$ 的映射；另一方面，当编码维数为 $q-1$ 时，也可以将 RS 码视为多项式到多项式的映射，即 $f(x) \rightarrow c(x)$

纠错算法

本节介绍 Reed Solomon 的 Berlekamp–Welch 算法。

1. 我们先表述纠错问题：

   • 设 $RS_q(\alpha,n,k)$ 为 RS 码，编码距离 $d=n-k+1$，纠错能力 $e\leq\lfloor\frac{d-1}{2}\rfloor=\lfloor\frac{n-k}{2}\rfloor$
   • 设 $\overrightarrow{w}=(w_0,\cdots,w_{n-1})\in\mathbb{F}_q^n$ 为接收到的编码，且至多存在 $e$ 个错误
   • 求多项式 $f(x)\in\mathbb{F}_q[x]$ 使得：$\deg(f)\leq k-1$ 且至多存在 $e$ 个数值 $\alpha_i$，使得 $f(\alpha_i)\neq w_i$

2. 我们表述算法的过程，再论证细节：

   • 计算次数为 $e$ 的首一多项式 $E(x)$ 以及次数 $e+k-1$ 的多项式 $Q(x)$ 使得

   $$w_iE(\alpha_i) = Q(\alpha_i),\ \forall\ i=0,\cdots,n-1$$

   这里 $E(x)$ 称为错误检查多项式(Error locator polynomial)

   • 若找不到满足这一性质的多项式 $E(x)$ 和 $Q(x)$，则说明 $\overrightarrow w$ 超出了纠错范围
   • 令 $\tilde{f}(x)=Q(x)/E(x)$，若 $\Delta(\tilde{f},w)\leq e$，则 $f$ 为所求，否则说明 $\overrightarrow w$ 超出了纠错范围。这里 $\Delta(\tilde{f},w)$ 为满足 $\tilde{f}(\alpha_i)\neq w_i$ 的 $i$ 的个数

3. 我们先证明，若 $w$ 在纠错范围内，则满足性质的多项式 $E(x)$ 和 $Q(x)$。设 $f$ 为原始信息，如下定义 $E(x)$ 和 $Q(x)$

   $$\begin{align*} E(x) &= \prod_{i:f(\alpha_i)\neq w_i}(x-\alpha_i)\cdot x^{e-\Delta(f,w)}\\ Q(x) &= E(x)\cdot f(x) \end{align*}$$

   当 $f(\alpha_i)\neq w_i$ 时，

   $$w_iE(\alpha_i)=Q(\alpha_i)=0$$

   当 $f(\alpha_i)=w_i$ 时，亦有

   $$Q(\alpha_i)=E(\alpha_i)f(\alpha_i)=w_iE(\alpha_i)$$

4. 另一方面，若存在另一组 $Q'(x),E'(x)$ 满足同一性质，我们断言

   $$Q'(x)/E'(x)=Q(x)/E(x)$$

   换言之，即证

   $$R(x)=Q(x)\cdot E'(x)-Q'(x)\cdot E(x)=0$$

   注意到 $R(x)$ 的次数为

   $$\deg(R(x)= e+e+k-1\leq n-k+k-1<n$$

   然而 $R(x)$ 存在 $n$ 个根，继而 $R(x)=0$

   $$\begin{align*} R(\alpha_i)&=Q(\alpha_i)\cdot E'(\alpha_i)-Q'(\alpha_i)\cdot E(\alpha_i)\\ &=w_iE(\alpha_i)E'(\alpha_i)-w_iE'(\alpha_i)E(\alpha_i)\\ &=0,\quad \forall\ i=0,\cdots, n-1 \end{align*}$$

5. 结合两部分讨论，若 $w$ 在纠错范围内，满足这一性质的 $E(x)$ 和 $Q(x)$ 必然存在，且计算 $Q(x)/E(x)$ 立得原始信息 $f(x)$。若 $w$ 在纠错范围外，我们可以用同样方法尝试计算 $f(x)$ 并检验 $\Delta(f,w)$。（或许可以尝试证明不存在满足性质的 $E(x),Q(x)$）

6. 最后剩下关键问题，如何计算 $E(x),Q(x)$。

   • 待定 $E(x),Q(x)$ 的系数，根据多项式次数以及 $E(x)$ 首一性，变量数目为

   $$e+e+k\leq n-k+k=n$$

   代入$\alpha_i$，得到 $n$ 个等式构成的线性方程组

   $$Q(\alpha_i) = w_iE(\alpha_i),\ \forall i=0,\cdots,n-1$$

   根据前边讨论，该线性方程组无解或存在唯一解。若无解或解出的 $f(x)=Q(x)/E(x)$ 不满足要求，则表明 $w$ 在纠错范围外。

7. 最后，我们分析算法复杂度：

   • 解线性方程组：$O(n^3)$
   • 多项式除法：$O(n^2)$
   • 总计 $O(n^3)$

---

BCH 码

上节从范德蒙德矩阵出发定义 ReedSolomon 码，同时也提到，当 $n=q-1$ 时，RS 码具有更好的性质。本节从循环码的角度出发，给出这一情形 RS 码的等价定义。

循环码

1. 循环码为特殊的线性码，其满足在轮转下不变，换言之：

   $$(c_1,\cdots, c_{n}) \in C \Rightarrow (c_2,\cdots, c_{n},c_1)\in C$$

2. 循环码常用多项式给出，为此，我们回顾域扩张的结论：

   • 设 $f(x)$ 为多项式，则 $\mathbb{F}[x]$ 关于模 $f(x)$ 运算作成环，记为 $\mathbb{F}[x]/(f(x))$
   • 从环论角度，$\mathbb{F}[x]/(f(x))$ 为多项式环 $\mathbb{F}[x]$ 商主理想 $(f(x))$ 得到的环
   • 设 $f(x)$ 次数为 $k$，则 $\mathbb{F}[x]/(f(x))$ 的维数为 $k$，且容易取一组基元

   $$1, x, x^2,\cdots x^{k-1}$$

   • 商环 $\mathbb{F}[x]/(f(x))$ 为域当且仅当 $f(x)$ 为不可约多项式

3. 特别地，记 $R_n:=\mathbb{F}[x]/(x^n-1)$，其为 $n$ 维线性空间，且存在与 $\mathbb{F}^n$ 的自然同构

   $$\begin{align*} R_n&\rightarrow \mathbb{F}^n\\ \sum_{i=0}^{n-1}c_ix^i&\mapsto(c_0,\cdots,c_{n-1}) \end{align*}$$

   注意：从下文开始，在 $R_n$ 下，默认将多项式与向量等同看待。对 $R_n$ 上的多项式，左乘 $x$ 为轮转运算

   $$\begin{align*} x\cdot (c_0+c_1x+\cdots+c_{n-1}x^{n-1})&=c_{n-1}+c_0x+c_1^2+\cdots+c_{n-2}x^{n-1}\\ x\cdot(c_0,c_1\cdots, c_{n-1})&= (c_{n-1},c_0,\cdots,c_{n-2}) \end{align*}$$

4. 基于上一命题，我们给出 $R_n$ 上循环码的等价刻画：
   线性子空间 $C\subseteq R_n$ 为循环码当且仅当 $R_n.C\subseteq C$，即 $C$ 为 $R_n$ 的理想
   证明：
   若 $C$ 为循环码，则 $x\cdot C\subseteq C$，继而 $C$ 为 $R_n$ 的理想；反之，由 $x\cdot C\subseteq C$ 可得 $C$ 为循环码

5. 设 $I$ 为 $R_n$ 的理想，由辗转相除法可得

   $$f,g\in I\Rightarrow \gcd(f,g)=uf+vg\in I$$

   因而 $R_n$ 的所有理想均为主理想 $(d(x))$ 的形式

6. 推论：设 $C$ 为 $R_n$ 的循环码，则 $C=(d(x))$ 其中 $d(x)|x^n-1$
   证明：
   由上一命题，令 $d(x)$ 为 $C$ 所有多项式的最大公因子，则有 $C=(d(x))$；另一方面，$0=x^n-1\in C$，从而 $d(x)|x^n-1$

7. 通过获取 $x^n-1$ 的因子 $d(x)$，可以得到所有循环码，$d(x)$ 也称为 $C$ 的生成多项式(Generator polynomial)

8. 编码：设 $C=(g(x))$ 为 $R_n$ 的循环码，则块长为 $n$，信息长为 $k=n-\deg(g)$。具体地，我们通过以下映射给出编码

   $$\begin{align*} \mathbb{F}^k&\rightarrow R_n=\mathbb{F}^n\\ f(x)&\mapsto f(x)\cdot g(x)\mod x^n-1 \end{align*}$$

   这里 $f(x)$ 为次数小于 $k$ 的多项式，映射右侧利用关系 $x^n=1$ 进行降阶

9. 设生成元多项式

   $$g(x) = a_0+a_1x+a_2x^2+\cdots+a_{n-k}x^{n-k}$$

   则循环编码的矩阵为

   $$\begin{pmatrix} a_0&a_1&\cdots&a_{n-k}&0&\cdots&0&0\\ 0&a_0&a_1&\cdots&a_{n-k}&\cdots&0&0\\ \vdots&\ddots&\ddots&\ddots&\ddots&\ddots&\vdots&\vdots\\ 0&0&\cdots&a_0&a_1&\cdots&a_{n-k}&0\\ 0&0&\cdots&0&a_0&a_1&\cdots&a_{n-k} \end{pmatrix}^t$$

   由循环码特点，该矩阵列向量均在编码空间上，且矩阵秩为 $k$

10. 检错：设 $v(x)=c(x)+e(x)$ 其中 $c(x)$ 为数据码字，$e(x)$ 为错误信息，则

    $$v(x) = e(x)\mod g(x)$$

$v(x)$ 模 $g(x)$ 的余数多项式称为 syndrome polynomial，通过该多项式可以检查信息是否存在错误

本原循环码

下设 $\mathbb{F},\mathbb{K}$ 为以 $\mathbb{F}_p$ 为素域的有限域，且 $\mathbb{K}$ 为 $\mathbb{F}$ 的扩域。

1. 回顾域扩张的相关结论：

   • 域扩张 $\mathbb{K}/\mathbb{F}$ 为单扩张
   • 设 $\mathbb{K}=\mathbb{F}(\alpha)$ ，则 $\alpha$ 称为 $\mathbb{K}$ 在 $\mathbb{F}$ 上的本原元素
   • 等价地，本原元素 $\alpha$ 为 $\mathbb{K}^*$ 乘法群的生成元
   • 对任意 $\beta\in\mathbb{K}$，满足 $f(\alpha)=0$ 的次数最小的首一多项式 $f$ 称为 $\alpha$ 的极小多项式
   • 易见极小多项式均为不可约多项式($\mathbb{F}上$)
   • 设 $g(x)\in\mathbb{F}[x]$，则

     $$g(x) =LCM[g_1(x),\cdots,g_r(x)],\deg(g)=r$$

     其中 $g_i(x)$ 为 $g(x)$ 第 $i$ 个根的极小多项式
   • 本原元素 $\alpha$ 的极小多项式称为 $\mathbb{F}$ 上的本原多项式
   • 设 $f$ 为 $\mathbb{F}$ 上的本原多项式，则 $x$ 为 $\mathbb{K}=\mathbb{F}[x]/(f(x))$ 上的本原元素
   • 注1：不是所有不可约多项式均为本原多项式，由定义易见，本原多项式 = 单扩张为分裂扩张的多项式
   • 注2：环论上的本原多项式定义为系数互素的多项式（与域论版本无关，主要用与Gauss 引理）

2. 下设 $q=p^m, n=q-1$。设 $\{\beta_i\}_{i=1}^{q-1}$ 为域 $\mathbb{F}_{q}$ 上的非零元，则

   $$\begin{align*} x^{n}-1 = \prod_{i=1}^{q-1} (x-\beta_i) = \prod_{\beta\in\mathbb{F}_q^*} (x-\beta) \end{align*}$$

   • 注意到左侧为 $n$ 次多项式，而根据群阶 $\beta_i$ 为该多项式的 $n$ 个根，因而等式成立
   • $n=q-1$ 称为 $\mathbb{F}_p$ 上的本原块长(Primitive Block Length)
   • 将以 $n$ 为块长的循环码称为本原循环码(Primitive Cyclic Code)

3. 考虑 $R_n = \mathbb{F}_p[x]/(x^n-1)$ 上的循环码，根据上一节讨论，循环码由 $x^n-1$ 的因子给出，设

   $$x^n-1=f_1(x)\cdots f_r(x)$$

   其中 $f_i(x)$ 为不可约多项式，由分解可得，$R_n$ 的因子有 $2^r$ 个

4. 下边分析不可约因子 $f_i(x)$ 都有哪些

   • 根据前一式子，$\mathbb{F}_{p^m}$ 的所有非零元构成 $x^n-1$ 的所有根
   • 因而 $f_i(x)$ 均为某些根的极小多项式，我们将属于同一 $f_i(x)$ 的根称为相互共轭的
   • 设 $\beta\in\mathbb{F}_q^*$，则与 $\beta$ 共轭的元素为

   $$\{\beta, \beta^{p},\beta^{p^2},\cdots,\beta^{p^{s-1}}\}$$

   其中 $s$ 为使得 $\beta^{p^{s}}=\beta$ 成立的最小正整数
   证明：
   有限域为完备域，因而有域同构

   $$\begin{align*} \mathbb{F}_{q} &\rightarrow \mathbb{F}_{q}\\ x&\mapsto x^q \end{align*}$$

   该映射保持素域 $\mathbb{F}_p$ 不变，但将元素 $\beta$ 变为 $\beta^p$，因而 $\beta$ 与 $\beta^p$ 落在同一极小多项式上；另一方面，可以考虑用根与系数关系证明系数落在 $\mathbb{F}_p$ 上

   • 设 $\alpha$ 为域扩张 $\mathbb{F}_q/\mathbb{F}_p$ 的本原元素，此时设 $\beta=\alpha^t$，共轭集为

   $$\begin{align*} \{\alpha^t, \alpha^{t\cdot p},\alpha^{t\cdot p^2},\cdots,\alpha^{t\cdot p^{s-1}}\} \end{align*}$$

   根据循环群的性质，$t\cdot p^s\equiv 1\mod n$，换言之，可以通过计算 $p$ 在循环群 $\mathbb{Z}/(\frac nt\mathbb{Z})$ 中的阶数确定 $\alpha^t$ 极小多项式的次数

5. 举个例子，考虑 $\mathbb{F}_{2^3}$

   $$\begin{align*} x^7-1 &= (x-1)\cdot (x^3+x+1)\cdot(x^3+x^2+1)\\ &=(x-1)\cdot (x-\alpha)(x-\alpha^2)(x-\alpha^4)\cdot (x-\alpha^3)(x-\alpha^6)(x-\alpha^{12}) \end{align*}$$

   下边三部分与三个不可约多项式对应，其中 $\alpha^{12}=\alpha^5$

6. 设 $R_n$ 的循环码 $C$ 以 $g(x)$ 为生成元多项式。设 $c(x)=v(x)+e(x)\in\mathbb{F}_p$，其中 $v(x)$ 为数据编码，$e(x)$ 为噪声，设 $g(x)$ 的 $r$ 个根分别为 $(g_1, g_2,\cdots,g_r)$，则

   $$v(g_i) = c(g_i)+e(g_i)= e(g_i), \forall\ i\in\{1,\dots,r\}$$

   由此得到 $r$ 个等式，我们希望通过这些等式求解错误信息 $e(x)$

BCH 码

一般地，我们通过编码距离计算纠错能力，而 BCH 码相反，我们根据纠错位来设计编码。
相关内容参考笔记稿（后续整理博客）

相关链接

YouTube 视频：编码理论
Wiki 百科：Reed Solomon code
Wiki 百科：BCH Code
油管视频-Mary Wootters：Algebraic Coding Theory
油管视频：Information Theory, Coding and Cryptography