LeetCode 刷题笔记

唠唠闲话

本篇内容：位运算，二叉树遍历，二分查找，特殊数据结构，排序算法，最短路以及动态规划。

---

位运算

数环

1. 位运算逐位进行，可等同看成数环 $\mathbb{Z}_2^n$ ($\mathbb{Z}_2$ 直和环)上的运算

2. $\mathbb{Z}_2^n$ 为交换幺环，以 0 为零元， -1 为单位元（简记为 I），所有元素加法阶为 2

   位运算	数域操作
   异或运算 ^	环上加法
   与运算 &	环上乘法
   非运算 ~	~n 等同于 n ^ I
   或运算 |	a | b = a ^ b ^ (a & b)

   或运算推导过程如下：
   a | b = ~(~a & ~b) = I ^ (I ^ a) & (I ^ b) = a ^ b ^ (a & b)

3. 位运算左移 << 和 右移 >>

知识技巧

1. 异或技巧

   • 问题 136. 只出现一次的数字，利用 $\mathbb{Z}_2^n$ 元素加法阶为 2，将相等的数值抵消

   def singleNumber(nums: List[int]) -> int:
       from functools import reduce
       return reduce(lambda x, y: x ^ y, nums)

2. 减一技巧

   • 减一运算将最低位 1 化为 0，并将该位置以下的 0 化为 1，例如 11|1000 -> 11|0111
   • 延伸应用：n & n - 1 将最低位 1 以上不变，以下（含）全化 0，例如 11100 -> 11000 -> 10000 -> 0
   • 问题 231. 2 的幂，判断是否 2 的幂次

   # 当且仅当 n 为 2 的幂次时，数值化为 0
   def isPowerOfTwo(n: int) -> bool:
       return n > 0 and (n & n - 1) == 0

   • 问题191. 位1的个数

   # 每次进行 `n & n-1`，二进制数中的 1 数目减一
   def hammingWeight(n: int) -> int:
       ret = 0
       while n:
           n &= n - 1
           ret += 1
       return ret

3. 对偶地，加一技巧

   • 加一运算将最低位 0 化为 1，并将该位置以下的 1 化为 0，例如 110|011 -> 110|100
   • 延伸：n & n + 1 将最低位 0 以下的部分截断（化 0），例如 110|011 -> 11000

4. 分治技巧：

   • 构造 01 序列 s
   • 与运算 s & n 提取 n 在序列取值 1 的位置的信息，例如 1100 & n 提取四位整数 n 的前两位
   • 位移运算 >>, << 移动结果，例如 (1100 & n) >> 2 提取 n 的前两位，并移动到个位
   • 异或运算 ^ 合并提取内容，例如 (1100 & n) >> 2 ^ ((0011 & n) << 2) 将 n 的前两位与后两位交换

5. 分治应用题，190. 颠倒二进制位，图片来自负雪明烛
   

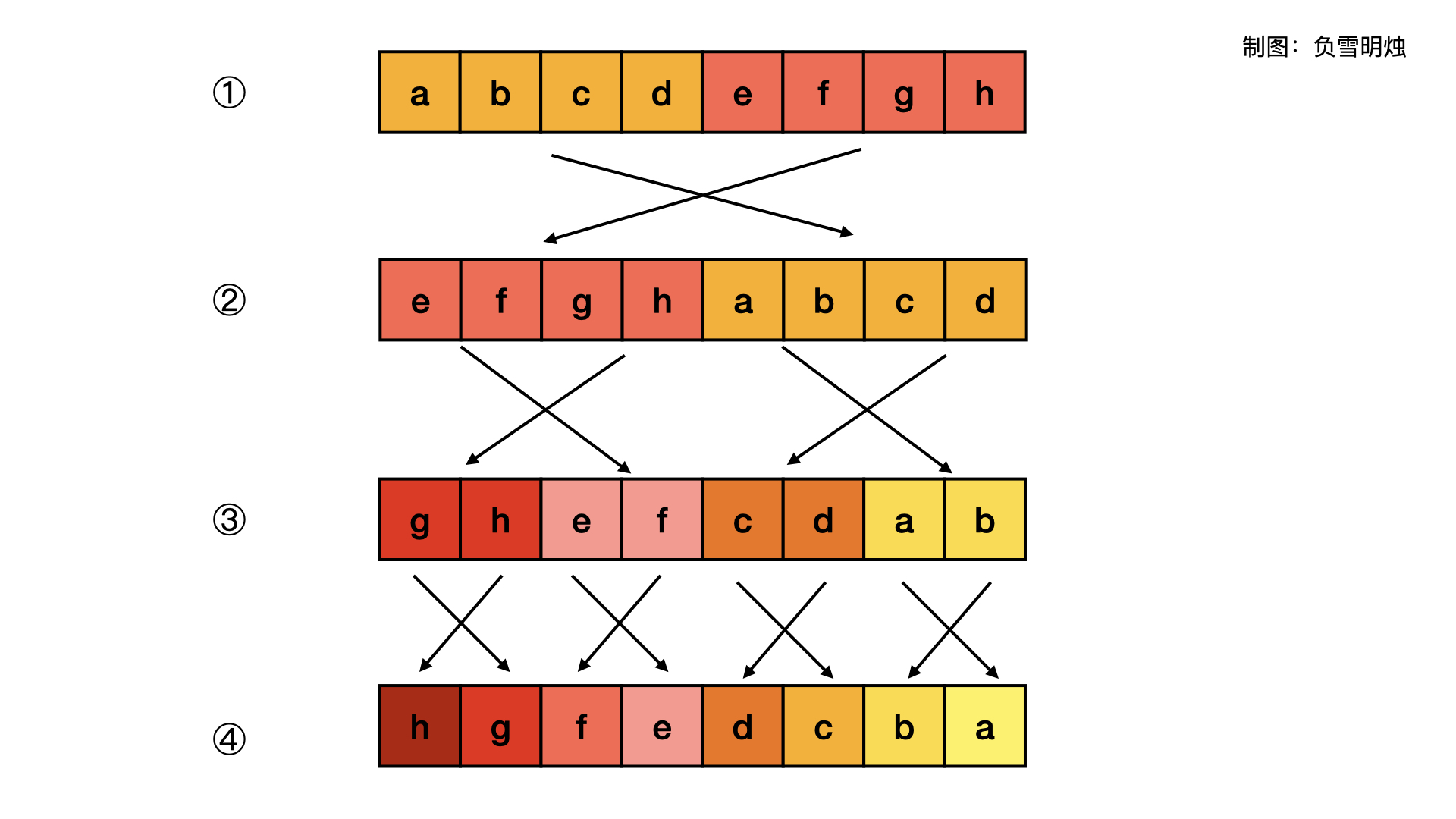
   • 利用分治思想，$32=2^5$ 位整数需互换 5 次，先理解 2,4,8 位的代码，再来看 32 位

   b = lambda i: int(i, 2)
   def reverse_bits_2(n: int)-> int:
       """二位整数互换"""
       return n >> 1 ^ (n << 1 & b("10")) # 10
   
   def reverse_bits_4(n: int)-> int:
       """四位整数互换"""
       n = n >> 2 ^ (n << 2 & b("1100")) # 1100
       n = n >> 1 & b("0101") ^ (n << 1 & b("1010")) # 10 的重复
       return n
   
   def reverse_bits_8(n: int)-> int:
       """八位整数互换"""
       n = n >> 4 ^ (n << 4 & b("11110000")) # 11110000
       n = n >> 2 & b("00110011") ^ (n << 2 & b("11001100")) # 1100 的重复
       n = n >> 1 & b("01010101") ^ (n << 1 & b("10101010")) ## 10 的重复
       return n
   
   def reverseBits(n: int) -> int:
       n = n >> 16 ^ (n << 16 & 0xffff0000) # 16 个 1
       n = n >> 8 & 0x00ff00ff ^ (n << 8 & 0xff00ff00) # 8 个 1
       n = n >> 4 & 0x0f0f0f0f ^ (n << 4 & 0xf0f0f0f0) # 11110000...
       n = n >> 2 & 0x03030303 ^ (n << 2 & 0xcccccccc) # 1100...
       n = n >> 1 & 0x55555555 ^ (n << 1 & 0xaaaaaaaa) # 1010
       return n

其他知识

1. 2, 8, 16 进制的单词分别为 binary, octal, hexadecimal，在 Python 中的相关函数如下

   # 十进制 -> 其他进制(字符串)
   bin(123) # '0b1111011' | 十进制 -> 二进制
   oct(123) # '0o173' | 十进制 -> 八进制
   hex(123) # '0x7b' | 十进制 -> 十六进制
   # 其他进制(字符串) -> 十进制
   int("011") # 11 | 十进制字符串 -> 十进制整数
   int("11", 3) # 4 | 三进制字符串 -> 十进制
   int("11", 2) # 3 | 二进制字符串 -> 十进制
   int("0b11", 2) == 0b11 # True | 可直接书写

2. 数值编码，参考 CSDN

   • 计算机中，有符号整数有三种存储方式，原码，反码和补码
   • 原码：用最高位表示符号位，‘1’表示负号，‘0’表示正号，其他位存放该数的二进制的绝对值
     • 整数 0 分为 +0 和 -0
     • 用原码做正负数的加法运算：0001 + 1001 = 1010 => 1 + (-1) = -2，出现问题
     • 原码虽然直观易懂，易于正值转换，但实现加减法的运算规则太复杂，于是反码来了
   • 反码：正数的反码还是等于原码，负数的反码就是他的原码除符号位外，按位取反
     • 比如 -3 = 1100, 0 = 0000 = 1111

     3 = 0(011) => -3 = 1(110) = 1100
     0 = 0(000) => -0 = 1(111) = 1111

     • 此时仍存在运算错误的问题

     1100 + 0001 = 1101 = -(0010) => -3 + 1 = -2
     1100 + 1001 = 1101 = -(0010) => -3 + (-6) = -2

   • 补码：负数的补码等于他的原码自右向做，第一个‘1’及其右边的‘0’保持不变，左边的各位按位取反
     • 等价刻画：正数的反码还是等于原码，负数的补码是其反码 + 1
     • 此外，正数和负数互为彼此的补码，0 的表达方式唯一

     0110 => -(0110) = 1010
     1010 => -(1010) = 0110
     0000 => 0000

     • 补码的数学运算

     # -1 + 1 = 0
     1111 + 0001 = 0000 # 进位丢掉
     # -2 + 1 = -1
     1110 + 0001 = 1111
     # -1 + 2 = 1
     1111 + 0010 = 0001

   • 由补码原理，负数位移运算 >> 也是下整除

   # 负数右移，左侧补 1
   # 1101 -> 1110 => -(0011) -> -(0010) => -3 -> -2
   -3 >> 1 == -2
   -1 >> 1 == -1 # 下整除

3. Python 位运算的优先级

   • 单目运算符 ~ 的优先级高于四则运算
   • >>, << 的优先级比 ==, !=, and, or, &, ^, | 高，比四则运算低

   1 == 1 << 1 # 返回 False
   2 or 1 << 2 # 返回 2，相当于 2 or 2
   (2 or 1) << 2 # 返回 8， 相当于 2 << 2
   1 + 2 << 3 # 返回 24，相当于 3 << 3
   1 & 1 << 3 # 返回 0，相当于 1 & 8
   (1 & 1) << 3 # 返回 8，相当于 1 << 3

4. Julia 位运算的优先级

   • >>, << 的优先级比 ==, !=, &&, ||, &, ⊻, | 高，与乘法运算同级
   • 也即： 1 + 2 << 3 在 Julia 中取值为 17，在 Python 中取值为 24

二叉树遍历

宽度优先遍历

树的三种宽度遍历方式，对应三道 LeetCode 习题：144. 二叉树的前序遍历，94. 二叉树的中序遍历，145. 二叉树的后序遍历

1. 先序遍历(Python)

   def traversal(root: TreeNode) -> List[int]:
       if not root: return []
       ans, stack = [], [root]
       while stack:
           node = stack.pop()
           ans.append(node.val)
           if node.right:
               stack.append(node.right)
           if node.left: # 左节点优先
               stack.append(node.left)
       return ans

2. 先序遍历 + 中序遍历(Julia)

   ## Julia 模板
   traversal(::Nothing) = Int[]
   function traversal(root::TreeNode)::Vector{Int}
       res, stack = Int[], []
       while !isempty(stack) || !isnothing(root)
           while !isnothing(root)
               push!(stack, root)
               ## preorder traversal
               root = root.left
           end
           root = pop!(stack) 
           ## inorder traversal
           root = root.right
       end
       res
   end

3. 先序遍历 + 中序遍历 + 后序遍历(Python)

   def Traversal(root: TreeNode) -> List[int]:
       if not root: return []
       res, stack, pre = [], [], None
       while root or stack:
           while root: # 访问到最左节点
               stack.append(root)
               # 先序遍历，准备访问左子树
               root = root.left
           root = stack[-1] # 到达最左节点
           if not root.right or root.right == pre: # 右节点为空或访问过
               # 后序遍历，左右子树访问完毕
               pre, root = stack.pop(), None
           else:
               # 中序遍历，准备访问右子树
               root = root.right
       return res

Morris 遍历

暂略，有需要再学习

序列构造树

递归解法比较简单，难点是迭代解法。

1. 先序遍历 + 中序遍历，反推二叉树，问题 105

   def buildTree(preorder: List[int], inorder: List[int]):
       root = TreeNode(preorder[0])
       stack, j, n = [root], 0, len(preorder)
       for i in range(1, n):
           node = TreeNode(preorder[i]) # 创建节点
           if stack[-1].val != inorder[j]: # 栈顶不是最左节点
               stack[-1].left = node
               stack.append(node) # 继续向左
           else: # 栈顶是最左节
               while len(stack) and inorder[j] == stack[-1].val: # 依次消除栈顶元素
                   j += 1
                   top = stack.pop()
               top.right = node # 合适位置向右
               stack.append(node)
       return root

2. 后序遍历 + 中序遍历，反推二叉树，问题 106
   （暂略）

二分查找

1. 自编模板，寻找左边界

   def search_left_border(left, right, key):
       """搜索 key(i)==true 的左边界"""
       ## e.g. search_left_border(0, 10, lambda i:i>3) | returns 4
       while left <= right:
           mid = (left + right) >> 1
           if key(mid): # 位置正确
               right = mid - 1
           else:
               left = mid + 1
       return left

2. 使用函数库

   from bisect import bisect_left
   bisect_left([], 0) == 0
   bisect_left([1, 2, 2], 2) == 1

特殊数据结构

前缀树

1. 简单说，就是根据输入的字符信息，构造多叉树，比如输入单词 "sea","sells","she"（图片来自 huwt）
   

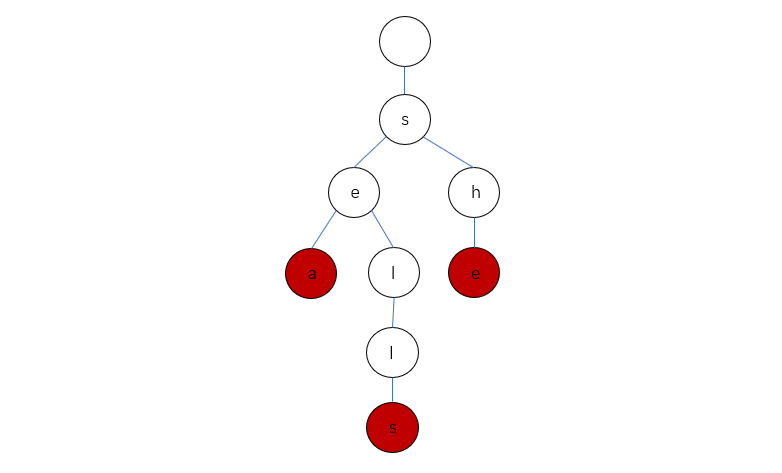
2. 树本身不存储信息，每次检查单词时，根据能否切换分支进行判断，具体问题可以添加结尾标记 isend = true 等信息。

3. 相关 LeetCode 问题：前缀树 208，最长前缀 720

4. 习题 720，给出单词列表中，逐步添加得到的最长单词（Julia 代码）

   function longest_common_word!(words::Vector{String})::String
       root, res = Dict{Char, Dict}(), ""
       for word in sort!(words, by=length)
           node, n = root, length(word)
           for (i, c) in enumerate(word)
               if haskey(node, c)
                   node = node[c]
               elseif i == n
                   node[c] = Dict{Char, Dict}() ## add new child
                   res = word
               else
                   break
               end
           end
       end
       res    
   end

线段树

线段树的三个关键步骤，对应 LeetCode 习题 307，计算可变数据的区间和

• 构造线段树
• 更新线段树
• 查找区间信息

1. 构造线段树

   • 将数据视为叶子节点
   • 根节点与左右子节点的索引关系为 k -> (2 * k, 2 * k + 1)
   • 根节点为左右子节点之和 nums[i] = nums[2 * i] + nums[2 * i + 1]
     Python 代码

   class SegmentTree:
       def __init__(self, nums: List[int]):
           self.n = n = len(nums)
           self.tree = tree = [0] * n + nums # 线段树 ST 长度为2n
           for i in range(n-1, 0, -1): # [1, n-1] 倒序添加，子节点之和
               # ST[2i] 和 ST[2i+1] 分别为 ST[i] 的左右子节点
               tree[i] = tree[i << 1] + tree[i << 1 | 1]

2. 更新索引信息，从叶子节点逐步往回

   def update(self, index: int, val: int) -> None:
       index += self.n # nums下标转换到 ST 下标
       delta = val - self.tree[index] # 变更值
       while index: # 自下而上进行更新
           self.tree[index] += delta
           index >>= 1
       return

3. 获取区间和

   def sumRange(self, left: int, right: int) -> int:
       # nums下标转换到 ST 下标
       left += self.n
       right += self.n
       res = 0
       while left <= right:
           if left & 1: # 奇数，右子节点
               res += self.tree[left]
               left += 1
           left >>= 1
           if right & 1 == 0: # 左子节点
               res += self.tree[right]
               right -= 1
           right >>= 1
       return res

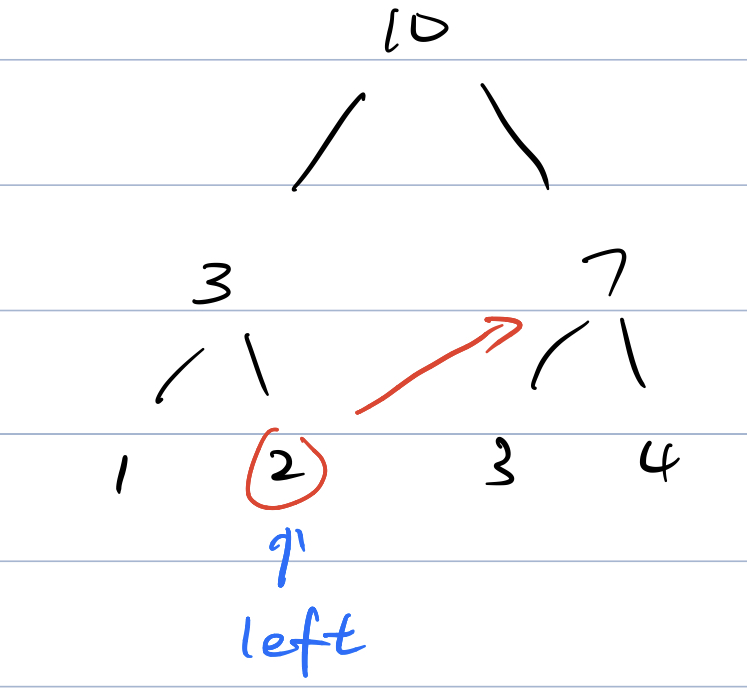
4. 原理说明，left 和 right 同步跳动，规则如下：

   • left 出现在左节点时，直接回退父节点
   • left 出现在右节点时，由于父节点也包含了左节点的结果，不能直接回退，而是记录当前数值，并跳到相邻父节点，如下图
     
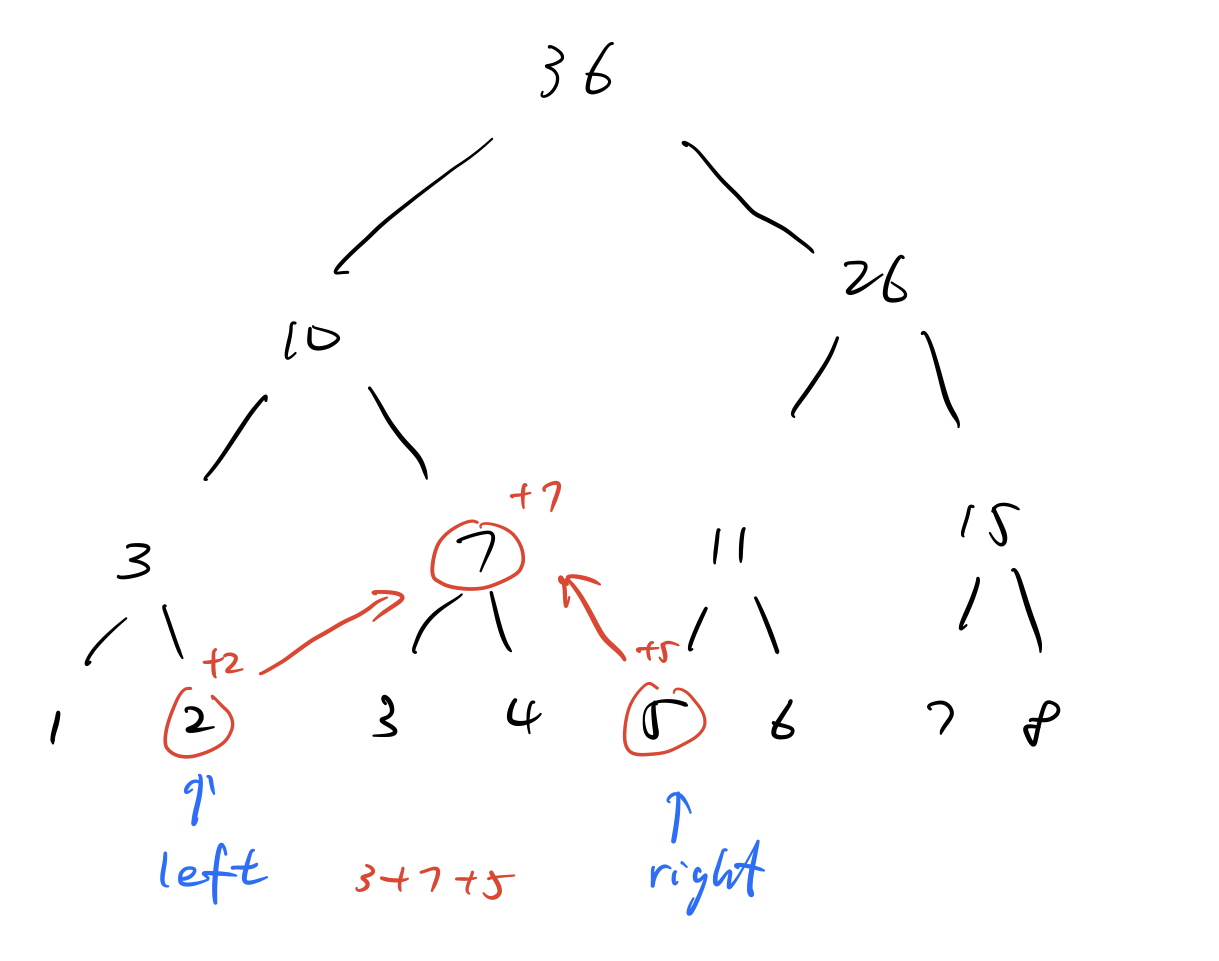
   • right 的规则与 left 相反，同理讨论
   • 当 right 和 left 相遇时，记录当前数值并跳出循环，如下图
     
   • 当 right 和 left 交错时，直接跳出循环，参看下图
     
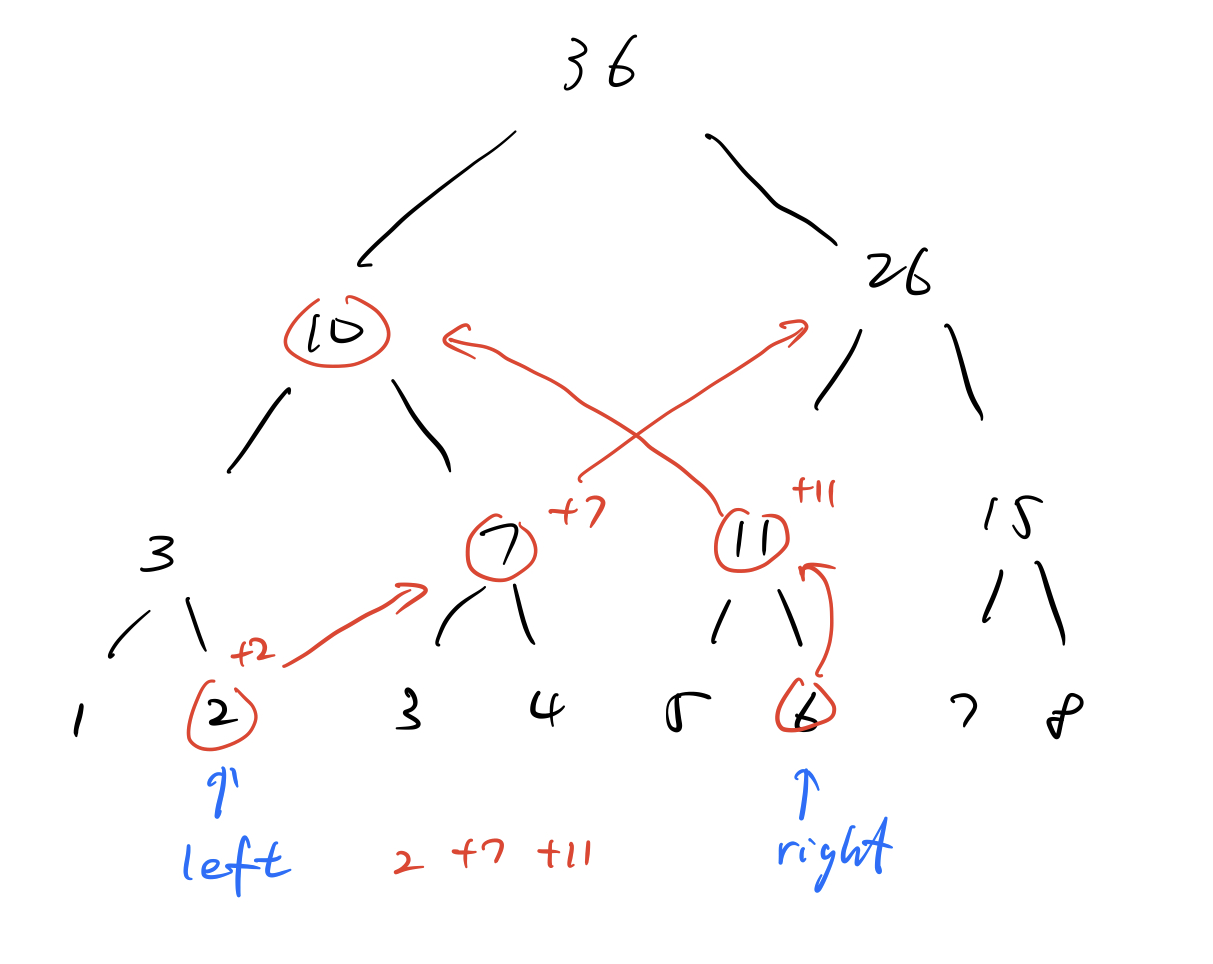
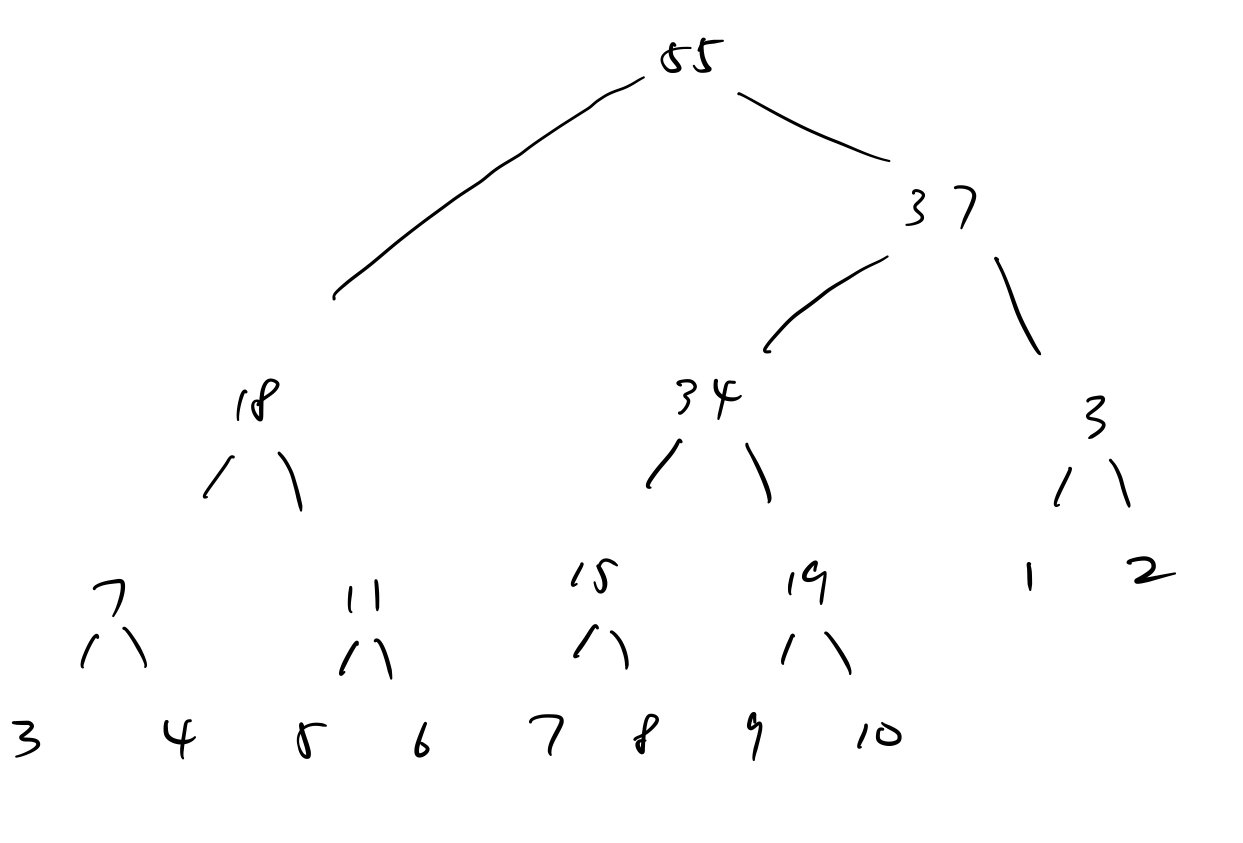
   • 讨论不仅对节点数目非 $2^n$ 的情形也适用，只是叶子节点会分布在两层，比如 10个节点的情形
     

排序算法

快速排序

1. 主函数

   def quick_sort(nums, left, right):
       if right <= left: return nums # 至少两个元素
       p = partition(nums, left, right)
       quick_sort(nums, p + 1, right) # 排序右边部分
       quick_sort(nums, left, p - 1) # 排序左边部分

2. 双边扫描，左指针数值保持严格小，右指针保持不小于

   def partition(nums, left, right):
       i, j, num = left, right - 1, nums[right] # 左右指针和中间值
       while i <= j:
           if nums[i] < num: # 左指针前进
               i += 1
           elif nums[j] >= num: # 右指针后退
               j -= 1
           else: # 交换
               nums[i], nums[j] = nums[j], nums[i]
               i, j = i + 1, j - 1
       nums[right], nums[i] = nums[i], nums[right]
       return i

3. 单边扫描，一个指针扫描，一个指针记录大于目标值的最左位置

   def partition(nums, left, right):
       p1, num = left, nums[right] # 记录位置的指针 p1
       for p2 in range(left, right): # 扫描区间 [left, right-1]
           if nums[p2] < num: # 小于目标值，交换到左侧
               nums[p1], nums[p2] = nums[p2], nums[p1]
               p1 += 1
       nums[p1], nums[right] = nums[right], nums[p1] # 最后交换目标值
       return p1

归并排序

1. 代码模板

   def merge_sort(arr):
       n = len(arr)
       if n <= 1: return arr
       mid = n >> 1
       lpart = merge_sort(arr[:mid])
       rpart = merge_sort(arr[mid:])
       return merge(lpart, rpart)
   
   def merge(lpart, rpart):
       tmp, i, j, nl, nr = [], 0, 0, len(lpart), len(rpart)
       while i < nl or j < nr:
           if j == nr or i < nl and lpart[i] <= rpart[j]:
               tmp.append(lpart[i])
               i += 1
           else:
               tmp.append(rpart[j])
               j += 1
       return tmp
   
   merge_sort(nums)

2. 相关 LeetCode 问题：

   • 剑指 Offer 51. 数组中的逆序对，在降低反序的位置记录数值
   • 问题 315. 计算右侧小于当前元素的个数，数据预处理，用 (idx, num) 形式记录索引

堆排序

小顶堆模板

from heapq import heapify, heappop, heappush, nsmallest, nlargest
heapify(nums)
nsmallest(1, nums)

最短路

堆优化的 Dijkstra 模板

def dijkstra(arrows, src, dist):
    """arrows 为字典类型"""
    queue = [(0, src)]
    dist[src] = 0
    while len(queue):
        cost, node = heappop(queue)
        if cost > dist[node]:continue
        for new, weight in arrows[node].items():
            weight += cost
            if weight < dist[new]:
                dist[new] = weight
                heappush(queue, (weight, new))
    return 

动态规划

01背包

暂略