Python 实战 | 十大排序算法

唠唠闲话

本篇用 Python 实现常见的排序算法，并分析计算复杂度，跳转目录：

常规方法：冒泡排序，选择排序，插入排序
特殊技巧：希尔排序，归并排序，快速排序
借助特殊数据结构：堆排序
分治和统计：计数排序，桶排序，基数排序

相关文章
五分钟学算法：算法与数据结构文章详细分类与整理！
VisuAlgo：数据结构动图生成
 十大经典排序算法（动图演示）
十大经典排序算法及比较与分析
 数据结构与算法：Learn DS & Algorithms

汇总比较

前 7 个排序算法基于比较，最后 3 个基于计数，不同算法在不同场景的优势不同。

$\begin{array}{|c|c|c|c|c|c|} \hline \textbf{排序算法}&\textbf{平均时间复杂度}&\textbf{最好情况}&\textbf{最坏情况}&\textbf{空间复杂度}&\textbf{稳定性}\\\hline \textbf{冒泡排序（优化后）}&O(N^2)&O(N)&O(N^2)&O(1)&稳定\\\hline \textbf{选择排序}&O(N^2)&O(N^2)&O(N^2)&O(1)&不稳定\\\hline \textbf{插入排序（直接）}&O(N^2)&O(N)&O(N^2)&O(1)&稳定\\\hline \textbf{插入排序（二分）}&O(NlogN)&O(NlogN)&O(NlogN)&O(1)&稳定\\\hline \textbf{希尔排序}&O(NlogN)&O(NlogN)&O(N^2)\ or\ less&O(1)&不稳定\\\hline \textbf{归并排序}&O(NlogN)&O(NlogN)&O(NlogN)&O(N)&稳定\\\hline \textbf{快速排序}&O(NlogN)&O(NlogN)&O(N^2)&O(logN)&稳定\\\hline \textbf{堆排序}&O(NlogN)&O(NlogN)&O(NlogN)&O(1)&不稳定\\\hline \textbf{计数排序}&O(N+k)&O(N+k)&O(N+k)&O(k)&稳定\\\hline \textbf{桶排序}&O(N)&O(N+k)&O(N^2)&O(N+k)&稳定\\\hline \textbf{基数排序}&O(N\cdot k)&O(N\cdot k)&O(N\cdot k)&O(N+k)&稳定\\\hline \end{array}$

其中希尔排序的复杂度分析比较复杂。

Ps：单从数据看，基于二分查找的插入排序表现最佳，但实际应用未必如此，比如归并排序可以顺带处理逆序数，堆排序常用于操作最大最小值。

以下代码部分自编，文字描述和动图演示转载自博客园和公众号。

冒泡排序

简介
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
动图演示

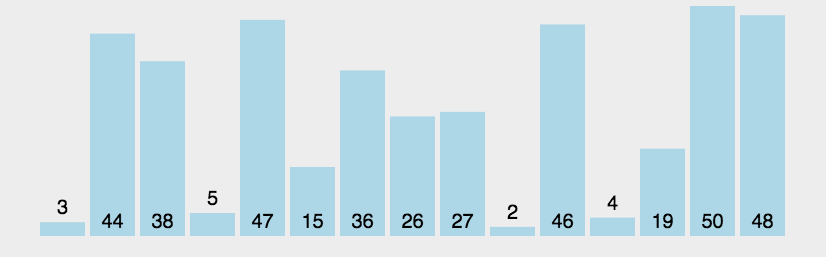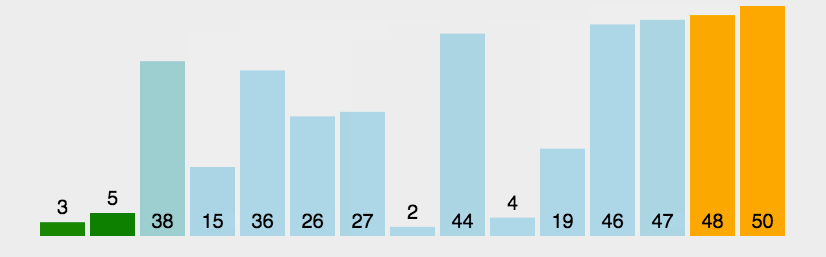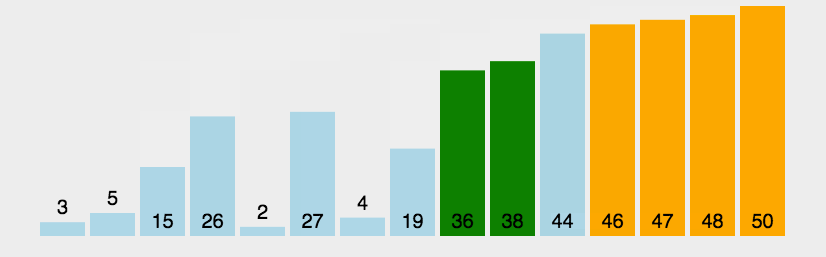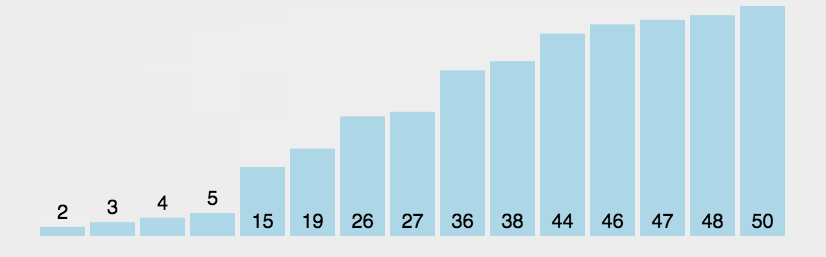
Python 代码（稳定排序）

def bubble_sort(nums):
    n = len(nums)
    for i in range(n - 1):
        is_sort = True
        for j in range(n - i - 1):
            if nums[j] > nums[j + 1]:
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
                is_sort = False
        if is_sort: # 提前跳出
            return nums
    return nums

算法复杂度：
- 空间复杂度： $O(1)$
- 最小时间复杂度（优化后）： $O(N)$
- 平均时间复杂度： $O(N^2)$
- 最坏时间复杂度： $O(N^2)$
编写技巧：
- 通过相邻元素比较，将较大值逐步移动到右侧
- 先排出最大值，然后次大值，依次下去

选择排序

简介
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
动图演示

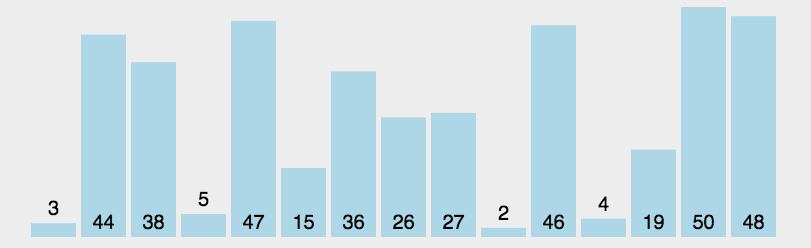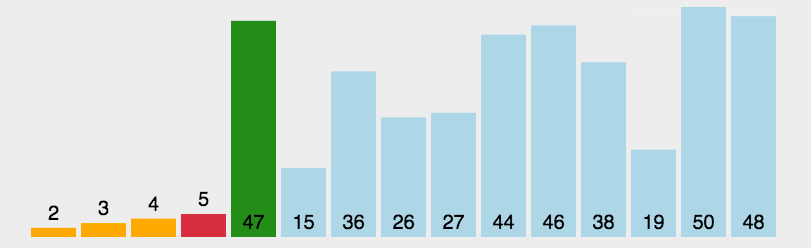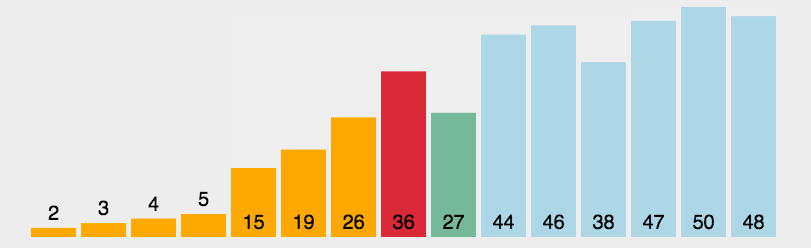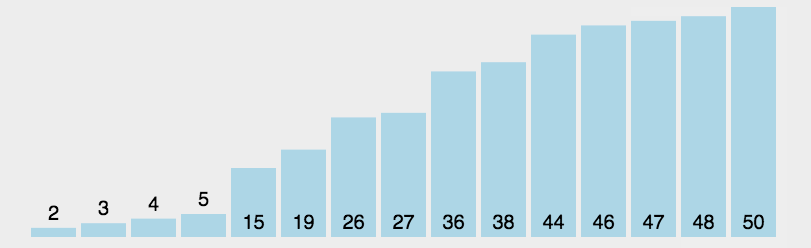
代码实现

def selection_sort(nums):
    n = len(nums)
    for i in range(n - 1):
        for j in range(i + 1, n):
            if nums[j] < nums[i]:
                nums[i], nums[j] = nums[j], nums[i]
    return nums

算法复杂度
- 空间复杂度： $O(1)$
- 最小时间复杂度： $O(N^2)$
- 平均时间复杂度： $O(N^2)$
- 最坏时间复杂度： $O(N^2)$
编写技巧
- 第 k 位置与 k + 1, k + 2, …, n 位置的元素比较，将较小者与第 k 位置交换
- 先排出最小值，然后次小值，依次下去

选择排序为不稳定排序，比如 [2,2,1] 交换导致 2 的相对位置改变

插入排序

简介
插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
动图演示

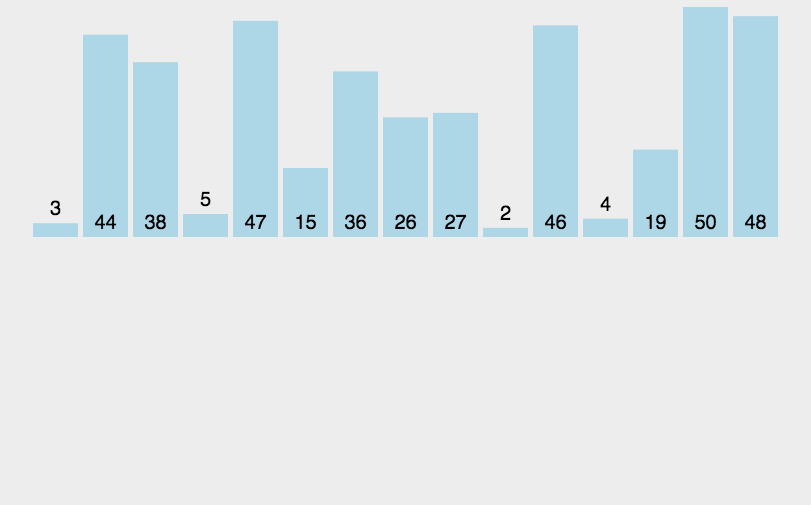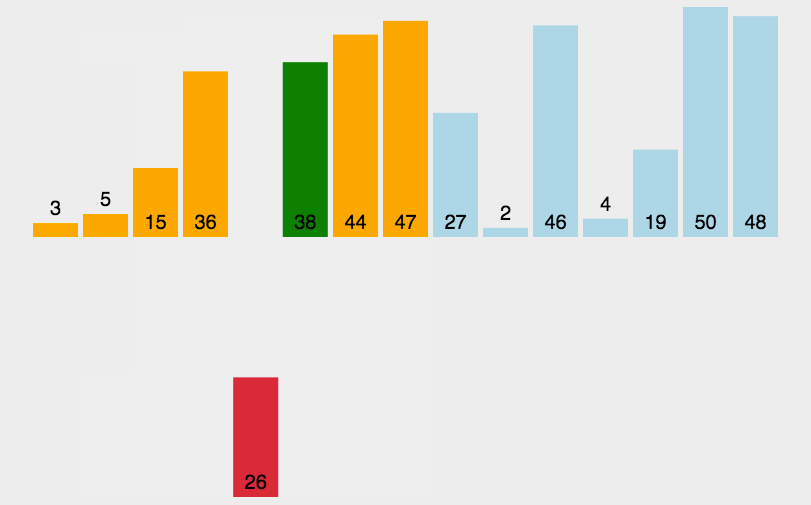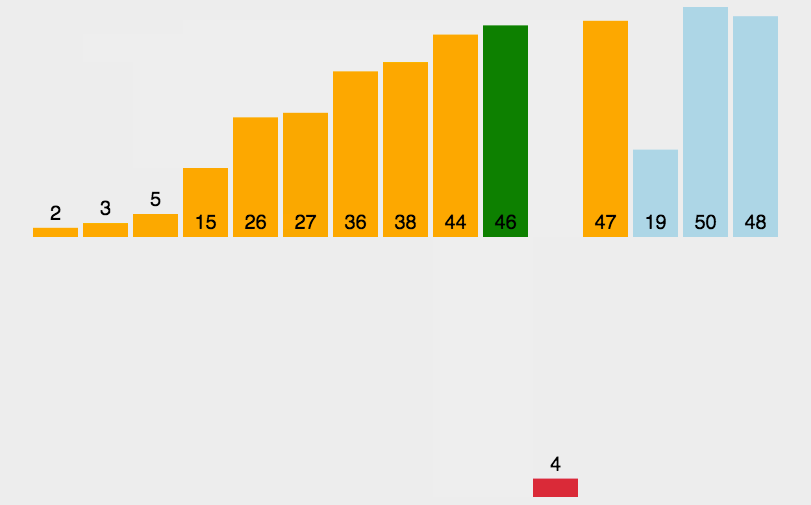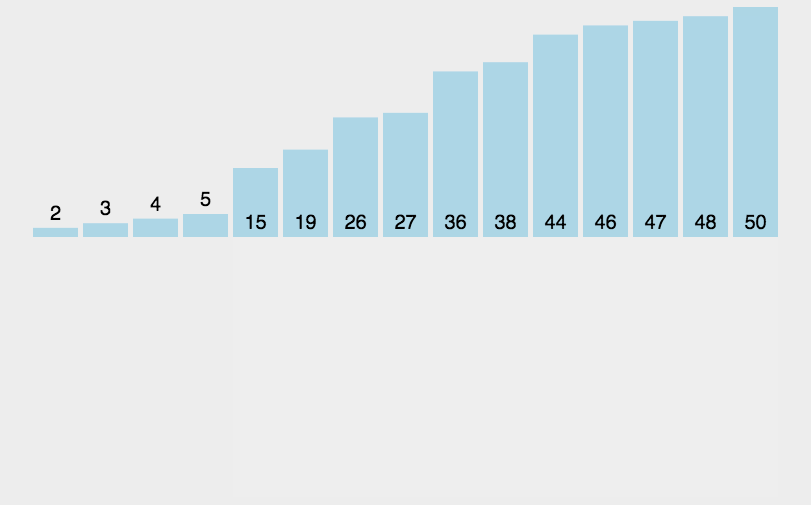
直接插入排序（稳定排序）

# 方法一：找到位置并插入
def straight_insertion_sort(nums):
    for i in range(1, len(nums)):
        num = nums.pop(i)
        for j in range(i - 1, -1, -1):
            if nums[j] <= num:
                nums.insert(j + 1, num)
                break
        else: # num is the minimal number
            nums.insert(0, num)
    return nums
# 方法二：逐次交换，最后插入
def straight_insertion_sort(nums):
    for i in range(1, len(nums)):
        for j in range(i, 0, -1):
            if nums[j - 1] > nums [j]:
                nums[j - 1], nums[j] = nums[j], nums[j - 1]
            else:
                break
    return nums

算法复杂度
- 空间复杂度： $O(1)$
- 最小时间复杂度： $O(N)$
- 平均时间复杂度： $O(N^2)$
- 最坏时间复杂度： $O(N^2)$

二分查找（稳定排序）

"""二分查找条件：<=target 的右侧"""
def bs_insertion_sort(nums):
    for i in range(1, len(nums)):
        num = nums.pop(i)
        left, right = 0, i - 1
        while left <= right:
            mid = left + ((right - left) >> 1)
            if nums[mid] <= num:
                left = mid + 1
            else:
                right = mid - 1
        nums.insert(left, num)
    return nums

算法复杂度
- 空间复杂度： $O(1)$
- 最小时间复杂度： $O(NlogN)$
- 平均时间复杂度： $O(NlogN)$
- 最坏时间复杂度： $O(NlogN)$
编写技巧
- 先让前 k 个元素有序，然后让前 k + 1 个有序，依次下去，直到整个数组有序
- 每一步将第 k + 1 个元素插入到 k 元有序数组的合适位置
- 插入方式有三种：
  1. 相邻比较 + 交换，将第 k + 1 个逐步移动到正确位置（静态数组）
  2. 将元素弹出，从后往前搜索到正确位置，再将元素插入（动态数组）
  3. 将元素弹出，用二分查找搜索正确位置，再将元素插入（动态数组）

希尔排序

简介
1959 年 Shell 发明，第一个突破 $O(N^2)$ 的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
动图演示

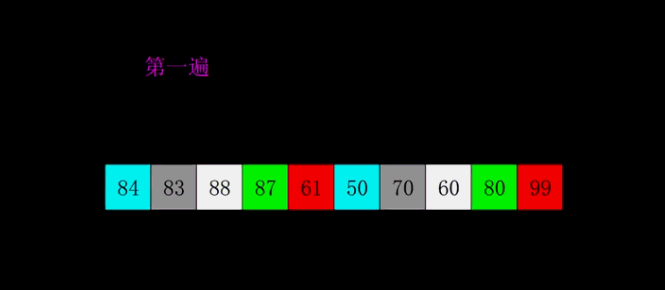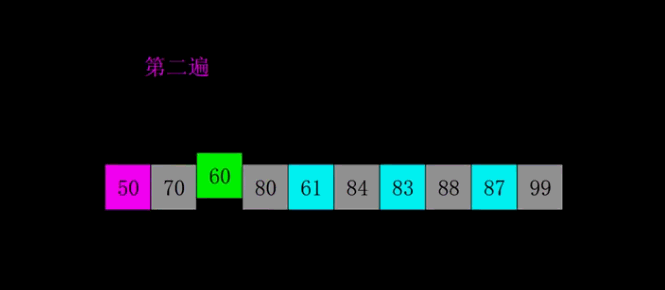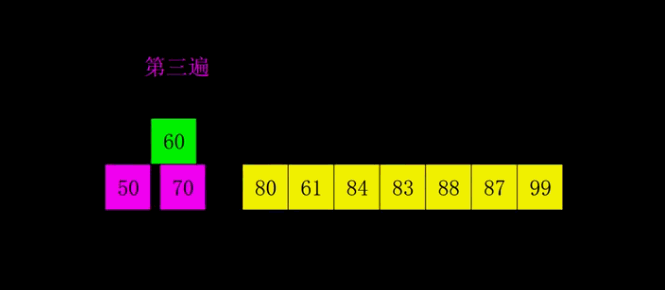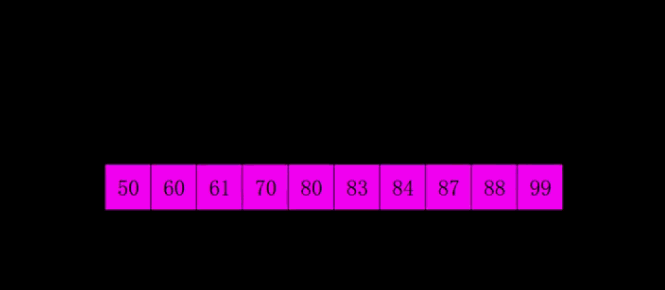
代码实现（不稳定排序）

def shell_sort(nums):
    n = len(nums)
    interval = n // 2
    while interval > 0: # logN times
        for i in range(interval, n):
            for j in range(i, interval - 1, -interval):
                if nums[j - interval] > nums[j]:
                    nums[j], nums[j - interval] = nums[j - interval],nums[j]
                else:
                    break
        interval //= 2
    return nums

注：虽然原理用分组演示，实际实现是多个组交错

算法复杂度
- 空间复杂度： $O(1)$
- 最小时间复杂度： $O(NlogN)$
- 平均时间复杂度： $O(NlogN)$
- 最坏时间复杂度： $O(N^2)$
编写技巧
- 拆分成 logN 次插入排序，每次使用相邻交换的方式进行
- 步长从半长开始，逐次减半，根据步长排序若干子数组
- 实际的代码实现是：多个子数组轮流进行，即 for i in range(interval, n)

归并排序

简介
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。
动图演示

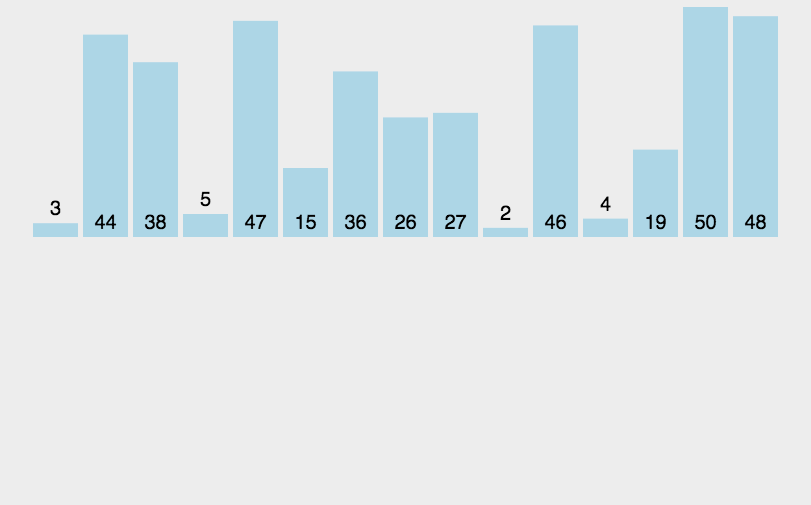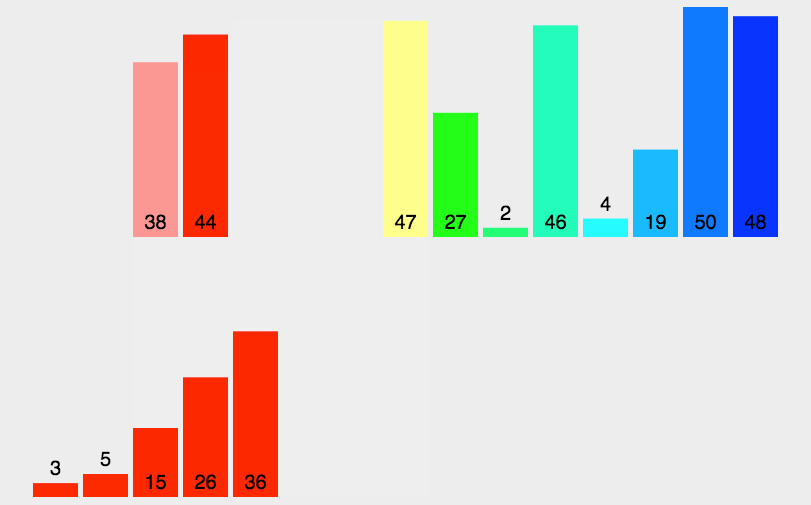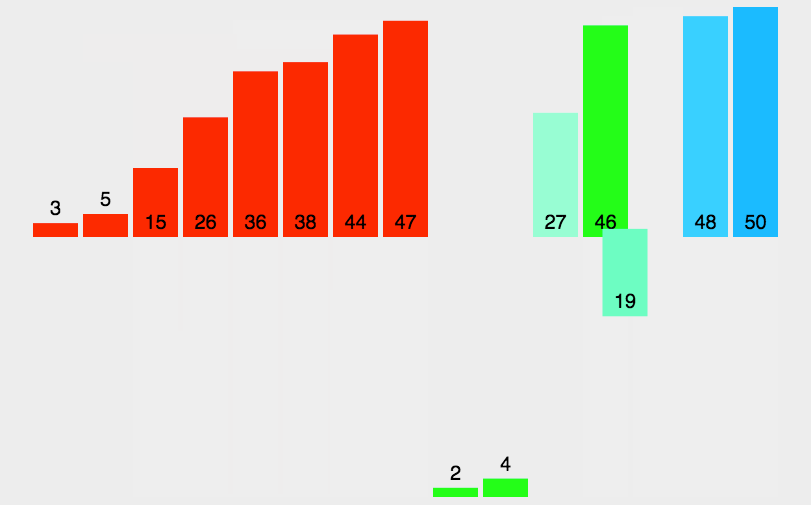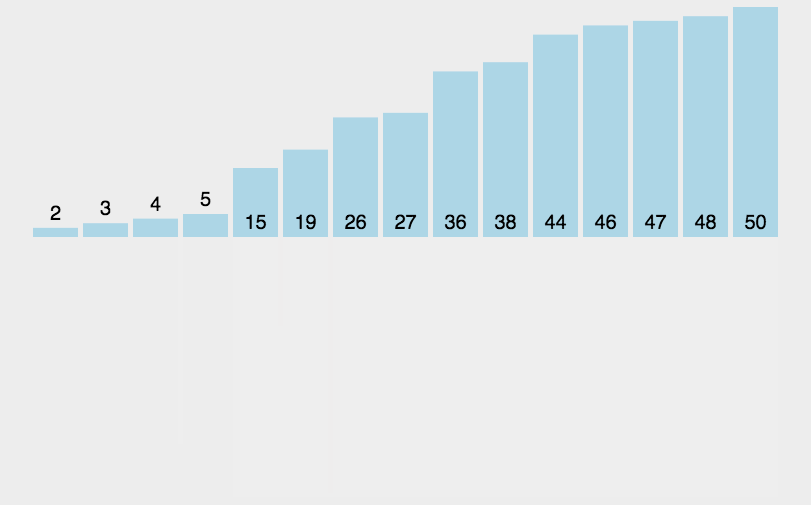
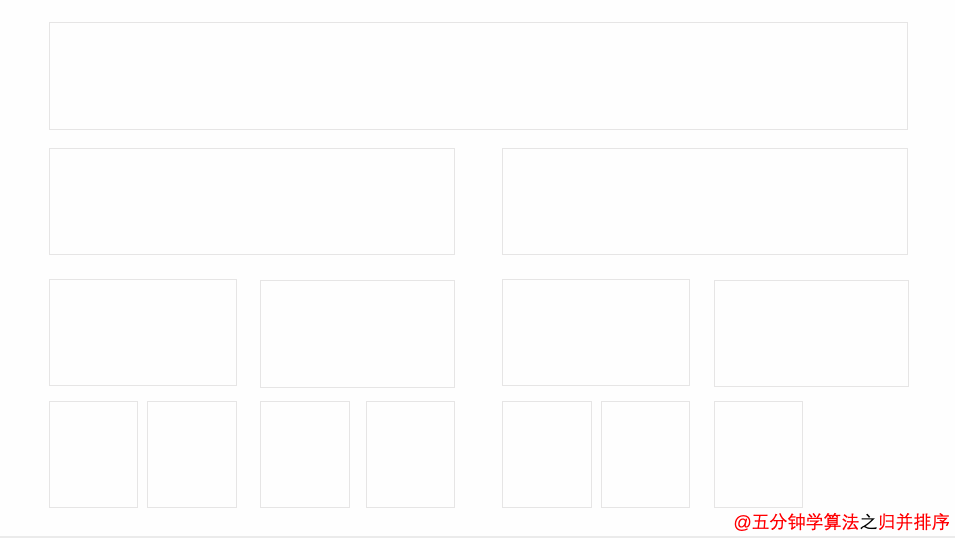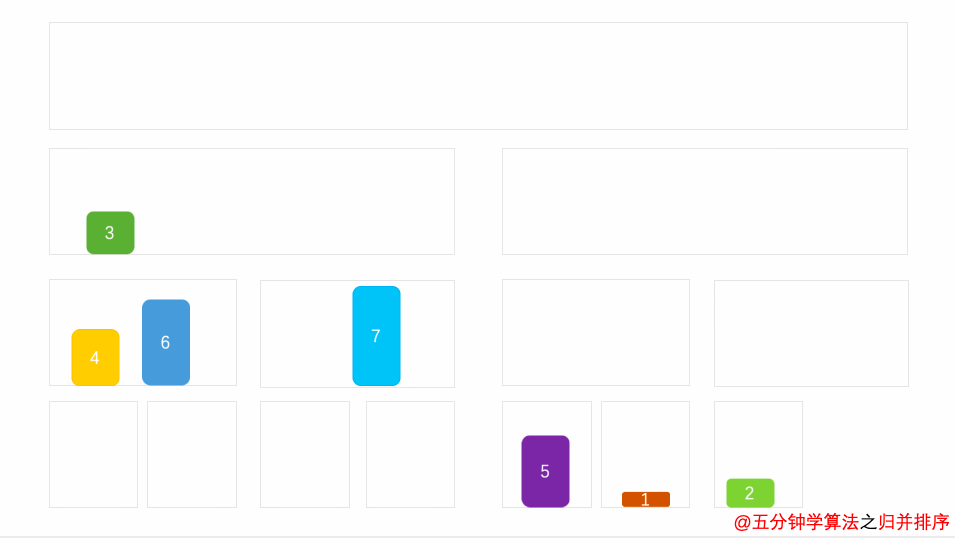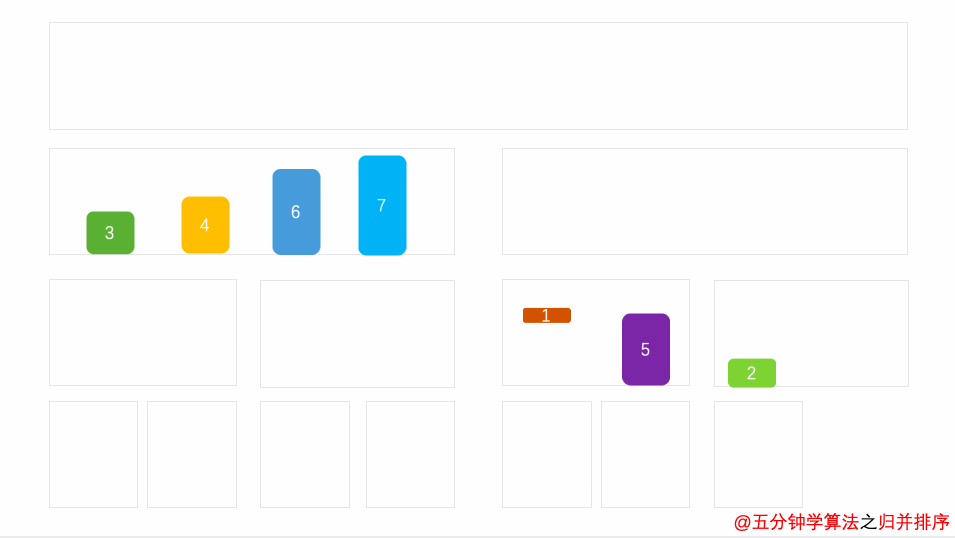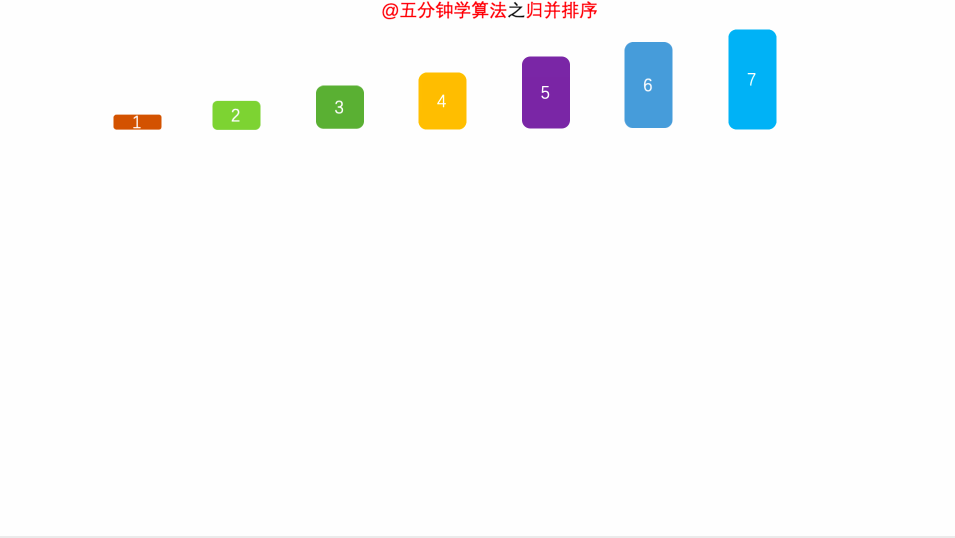
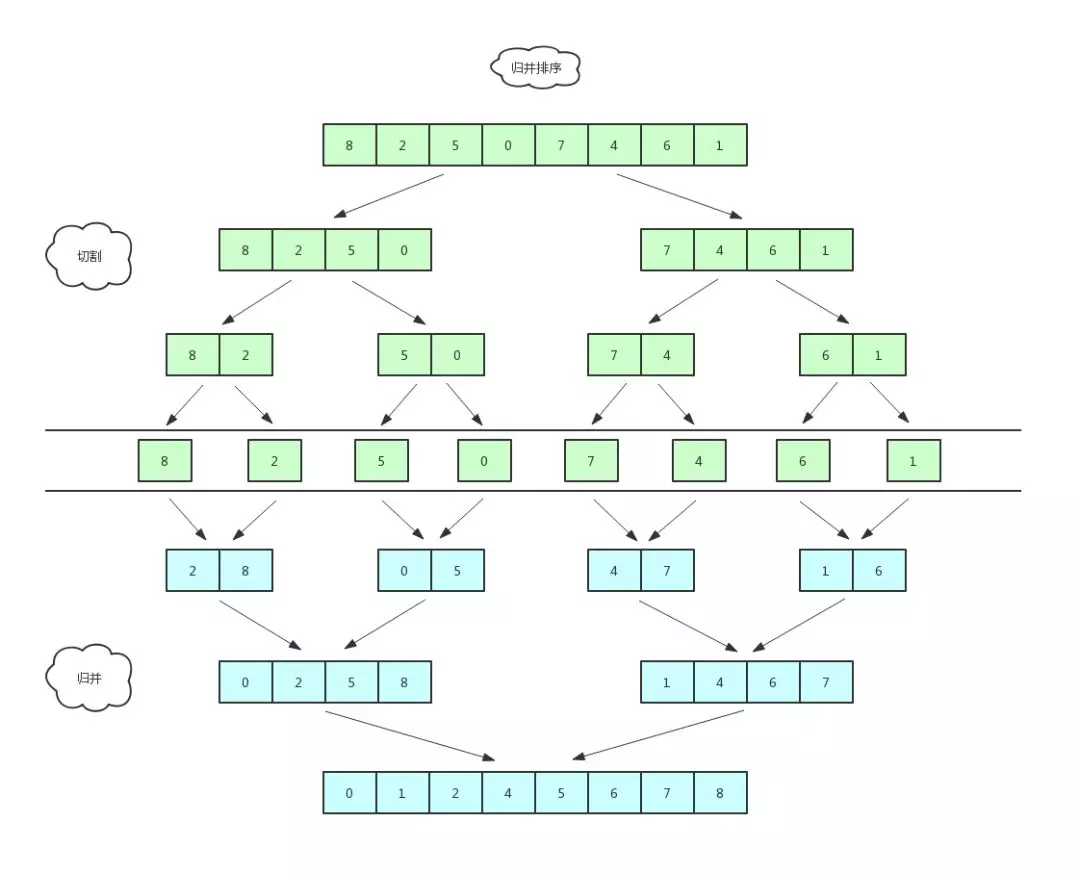
代码实现（稳定排序）

# 方法一：创建新数组
def merge_sort(nums):
    if len(nums) <= 1: # 边界情况
        return nums
    n = len(nums) // 2
    left, right, nums = merge_sort(nums[:n]), merge_sort(nums[n:]), []
    while len(right) and len(left):
        nums.append(left.pop(0) if left[0]<right[0] else right.pop(0))
    nums.extend(left), nums.extend(right)
    return nums

# 方法二：原数组上修改
def merge_sort(nums):
    n = len(nums)
    if n <= 1: # 边界情况
        return nums
    i, half = 0, n // 2
    left, right = merge_sort(nums[:half]), merge_sort(nums[half:]) # 两段内容需要复制
    for i in range(n):
        if not len(right) or not len(left): # 一侧为空时跳出
            break
        nums[i] = left.pop(0) if left[0] <= right[0] else right.pop(0)
    remain = left if len(left) else right
    for j in range(i, n):
        nums[j] = remain[j - i]
    return nums

算法复杂度（空间换时间）
- 空间复杂度： $O(N)$
- 最小时间复杂度： $O(NlogN)$
- 平均时间复杂度： $O(NlogN)$ 递归 $logN$ 层，每一层 $O(N)$ 时间
- 最坏时间复杂度： $O(NlogN)$
编写技巧
- 通过递归调用，化归为两个有序数组的排序问题
- 用双指针方法，通过比较左侧逐步排序

快速排序

简介
快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。
动图演示

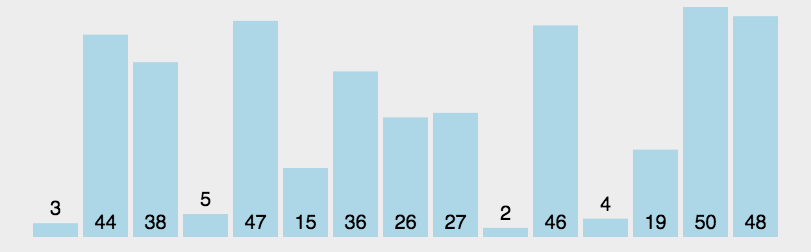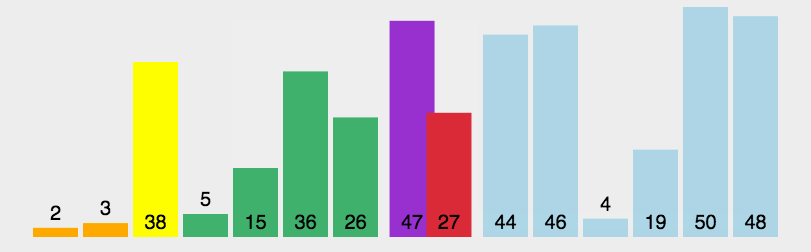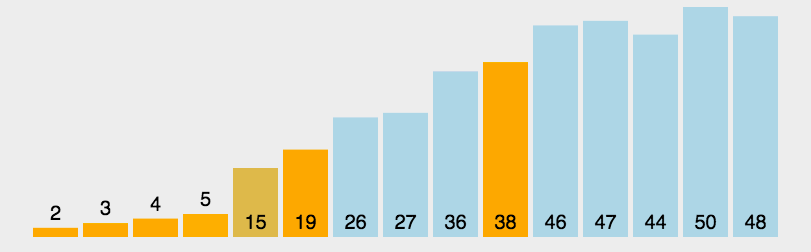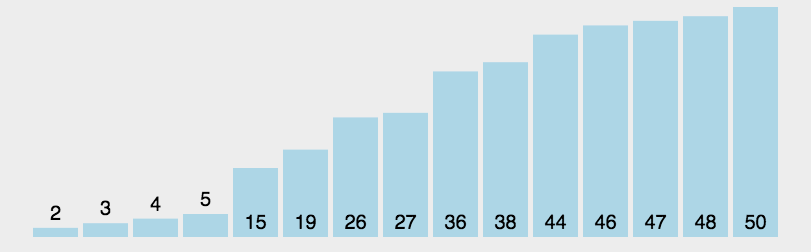
代码实现：双边扫描和单边扫描，均为不稳定排序

# 双边扫描，左指针保持严格小，右指针保持不小于
def partition(nums, left, right):
    i, j, num = left, right - 1, nums[right] # 左右指针和中间值
    while i <= j:
        if nums[i] < num: # 左指针前进
            i += 1
        elif nums[j] >= num: # 右指针后退
            j -= 1
        else: # 交换
            nums[i], nums[j] = nums[j], nums[i]
            i,j = i + 1, j - 1
    nums[right], nums[i] = nums[i], nums[right]
    return i

# 单边扫描，一个指针扫描，一个指针记录当前大于目标值的位置
def partition(nums, left, right):
    p1, num = left, nums[right] # 记录位置的指针 p1
    for p2 in range(left, right): # 扫描区间 [left, right-1]
        if nums[p2] < num: # 小于目标值，交换到左侧
            nums[p1], nums[p2] = nums[p2], nums[p1]
            p1 += 1
    nums[p1], nums[right] = nums[right], nums[p1] # 最后交换目标值
    return p1

def quick_sort(nums, left, right):
    if right <= left: return nums # 至少两个元素
    p = partition(nums, left, right)
    quick_sort(nums, p + 1, right) # 排序右边部分
    quick_sort(nums, left, p - 1) # 排序左边部分

注：相等可以当成小于处理，partition 返回值相应右挪。

算法复杂度
- 空间复杂度： $O(logN)$ 递归深度
- 最小时间复杂度： $O(NlogN)$
- 平均时间复杂度： $O(NlogN)$
- 最坏时间复杂度： $O(N^2)$ 每次选取值都是最大或最小
编写技巧
- 简便起见，每次取最右值作为目标值
- 关键步骤：将目标值填入正确位置，并调整使左侧数值小于目标值，右侧大于等于目标值，继而递归，实现方式有两种
- 单边扫描：
  - 双指针，指针 1 记录大于目标值的最左位置，指针 1 扫描
  - 从左往右扫，最后将目标值交换填入指针 2 位置
- 双边扫描：
  - 双指针，左指针保持严格小于目标值，右指针保持不大于目标值
  - 两侧往中间扫，左指针优先，当左右指针均不满足要求时，进行交换
  - 当指针相遇时，所在位置为目标值位置

堆排序

简介
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
动图及图片演示
最小堆的插入，时间复杂度 $O(logN)$

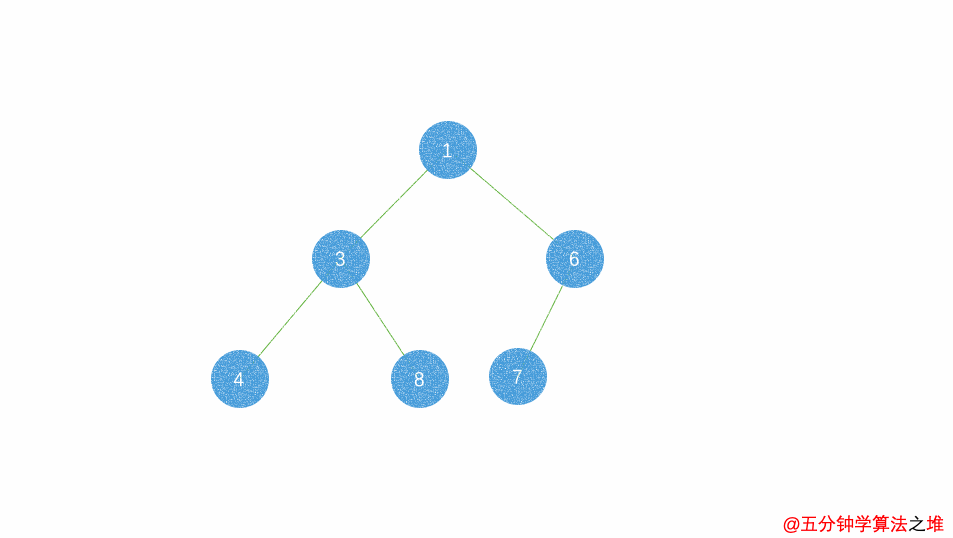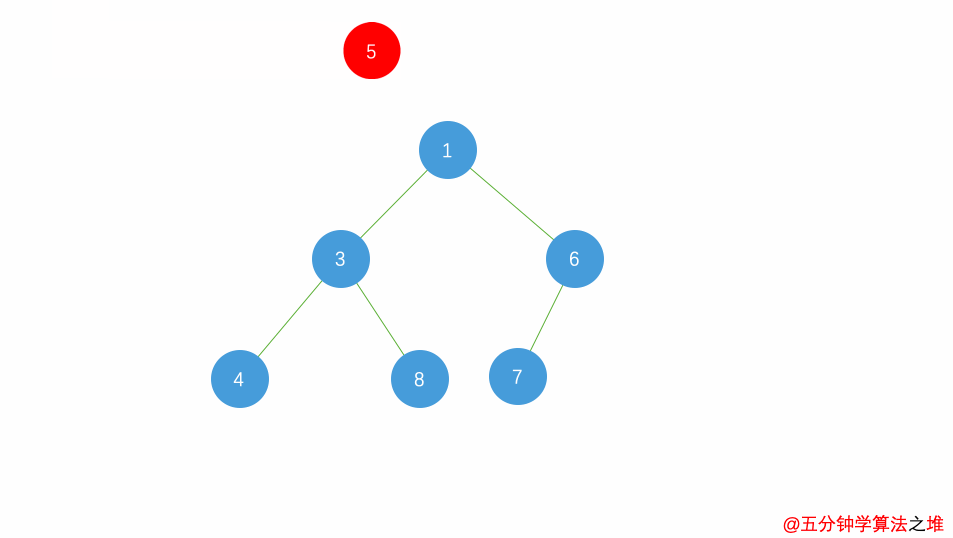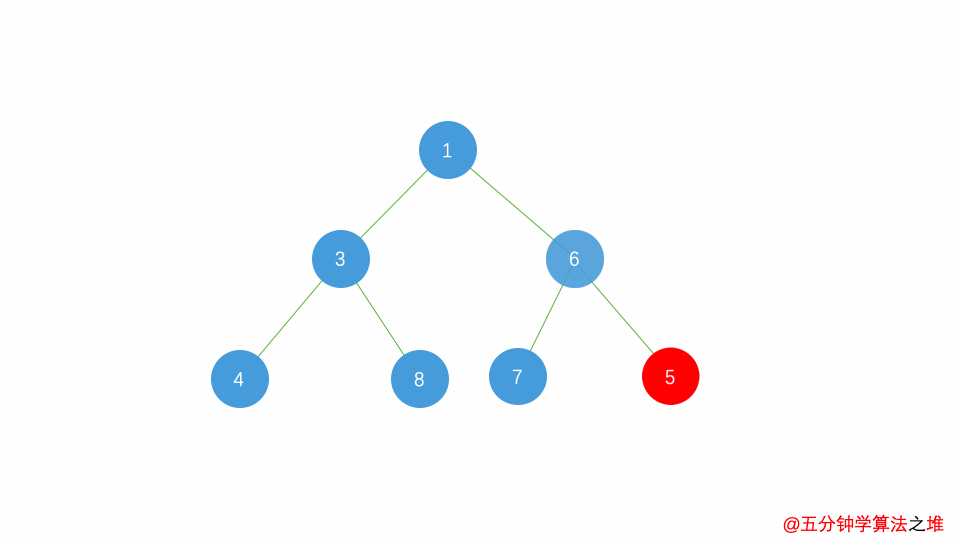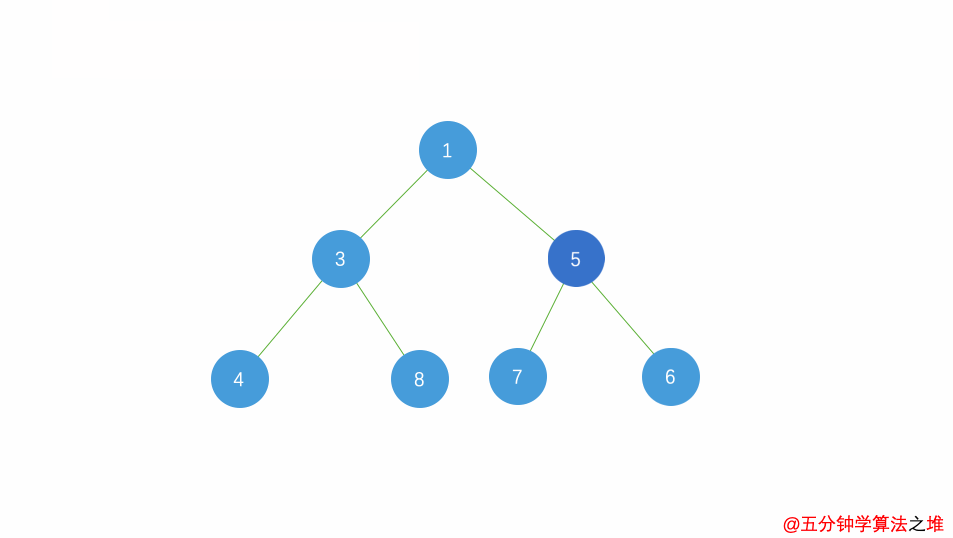
最小堆的删除，时间复杂度 $O(logN)$

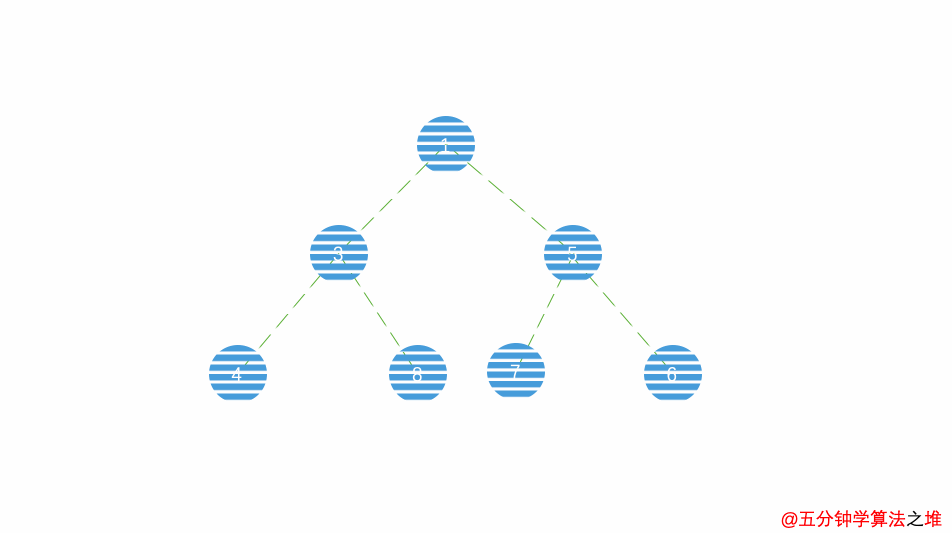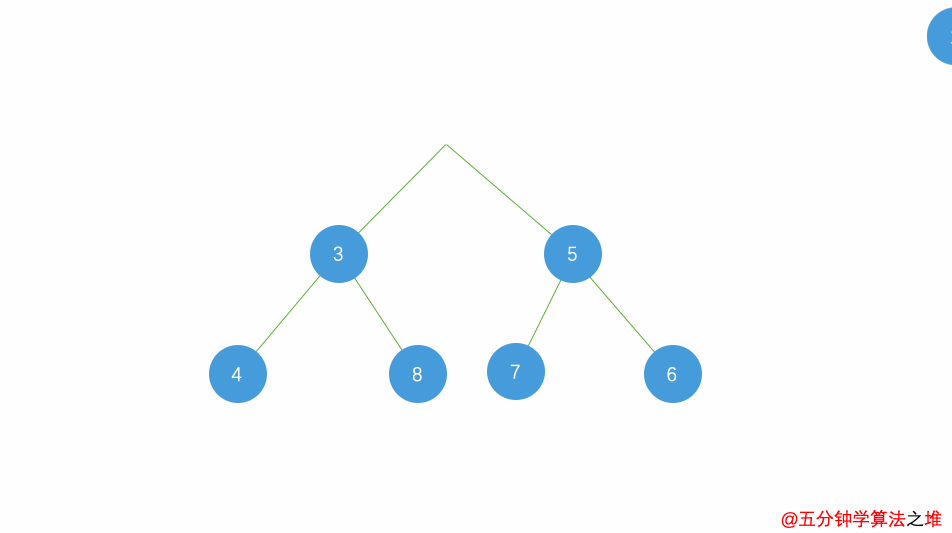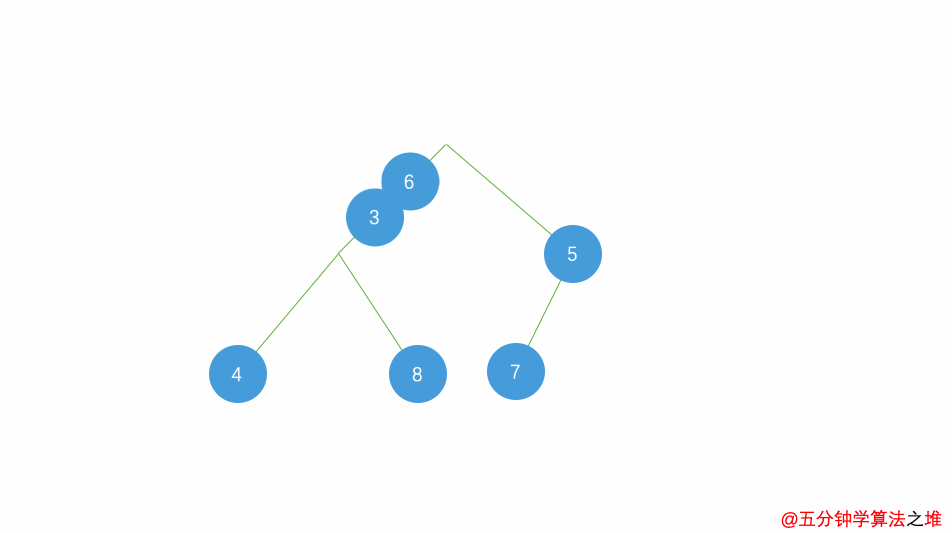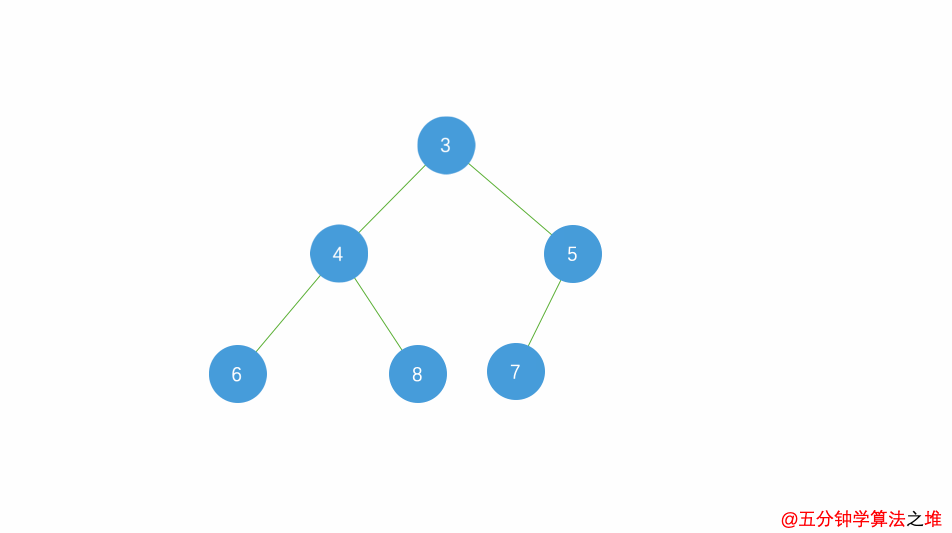
堆排序

代码实现（不稳定排序）

# 将 root 形成的子树变为有序状态
def heapify(nums, n, root) -> None:
    """假设 root 以下的节点已经有序，现处理 root 节点"""
    l, r = 2 * root + 1 ,2 * root + 2 # 左，右子节点
    # 求父节点，左节点和右节点三者中的最大
    largest = root 
    if l < n and nums[root] < nums[l]:
        largest = l
    if r < n and nums[largest] < nums[r]:
        largest = r
    if largest != root: # 最大点不是父节点，交换取值并递归
        nums[root], nums[largest] = nums[largest], nums[root]
        heapify(nums, n, largest)
    return

def heap_sort(nums):
    n = len(nums)
    for i in range(n // 2 - 1, -1, -1):
        heapify(nums, n, i)
    for i in range(n - 1, 0, -1):
        nums[i], nums[0] = nums[0], nums[i] # 首节点与末节点交换
        heapify(nums, i, 0)
    return nums

算法复杂度
- 空间复杂度： $O(1)$
- 最小时间复杂度： $O(NlogN)$
- 平均时间复杂度： $O(NlogN)$
- 最坏时间复杂度： $O(NlogN)$
编写技巧
- 将数组处理为大顶堆，每次将堆顶取出，堆尾补上，从后往前排序
- 末节点标号为 n-1，节点 m 的父节点为 (m-1)//2，左孩子 2*m+1，右孩子 2*m+2
- 堆化技巧：
  - 递归假设子树已堆化
  - 若当前节点和左右孩子构成的子树已经堆化，结束
  - 否则根节点与左右孩子中的最大者交换，并递归处理该子树
- 首次将数组堆化时，从后往前，递归处理非叶子节点

计数排序

简介
计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
动图演示

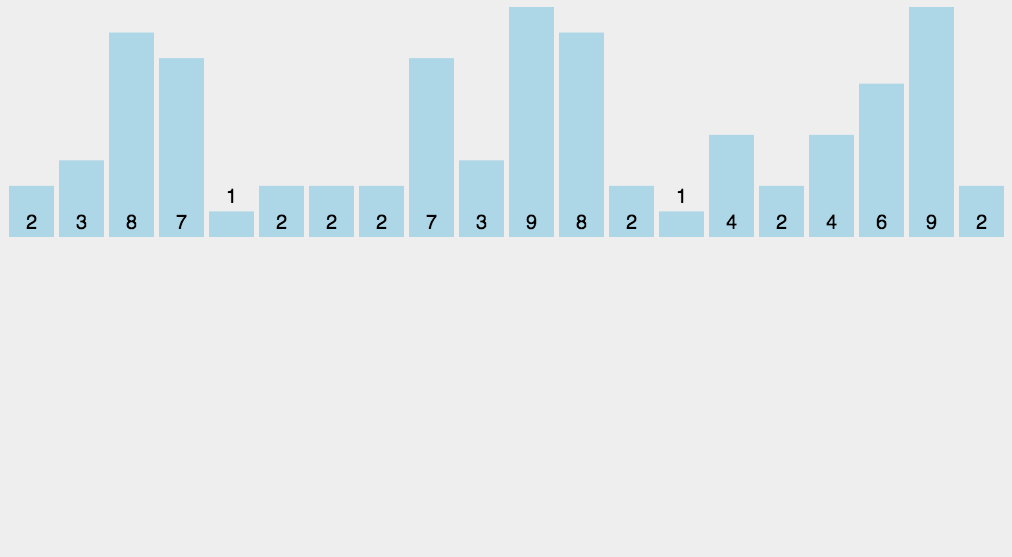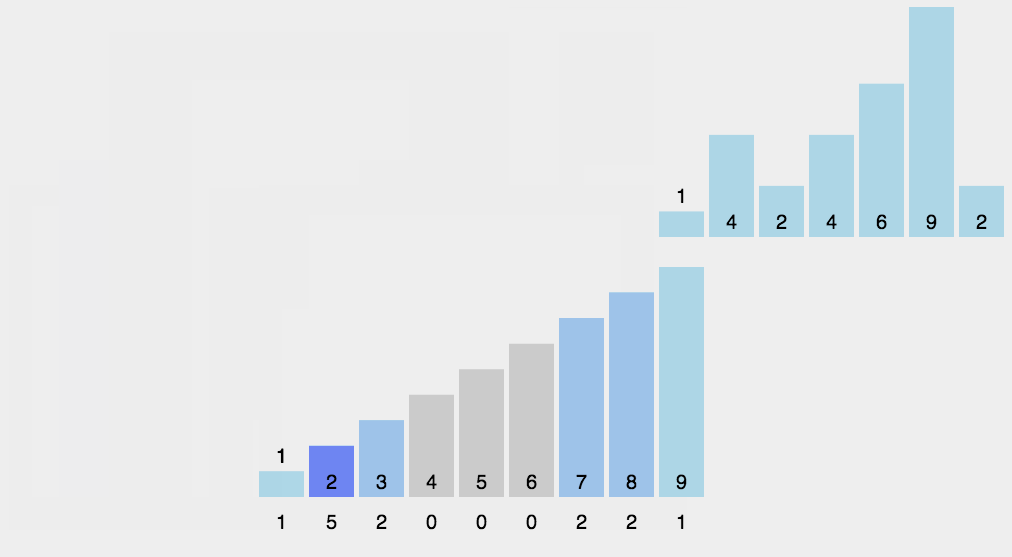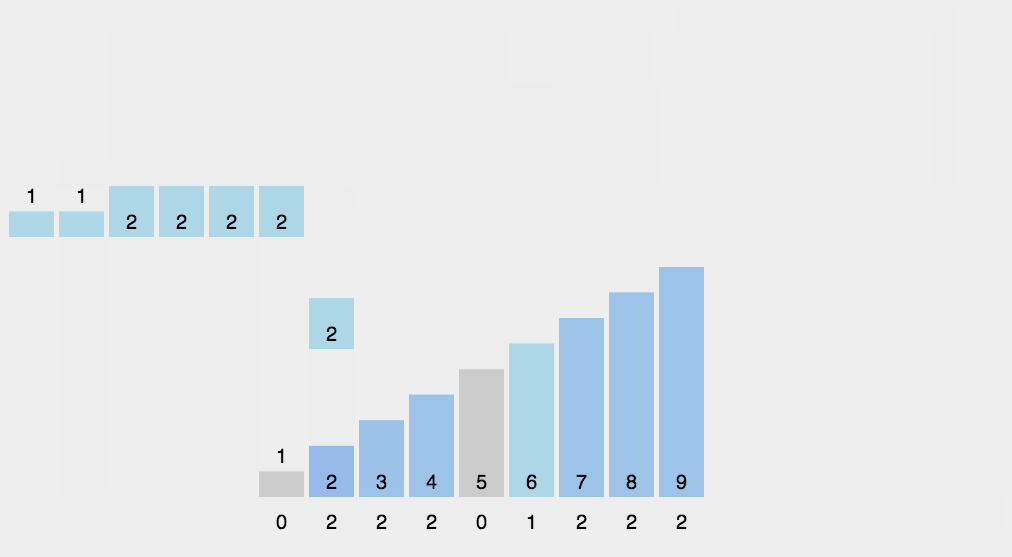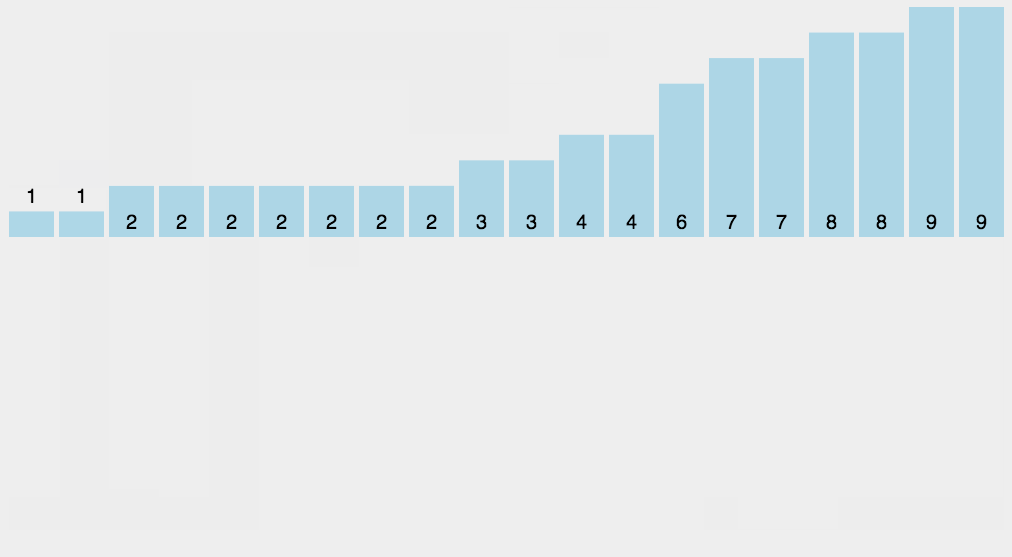
代码实现（稳定排序）

def counting_sort(nums):
    n = len(nums)
    if n==0: # 边界情形
        return nums
    # 最大最小值
    ma,mi = nums[0],nums[0]
    for i in range(1,n):
        if nums[i]>ma:ma = nums[i]
        elif nums[i]<mi:mi = nums[i]
    # 计数
    count = [0] * (ma - mi + 1)
    for i in nums:
        count[i-mi] += 1
    # 还原
    j = 0
    for i,num in enumerate(count):
        while num:
            nums[j] = mi + i
            num -= 1
            j += 1
    return nums

算法复杂度
- 空间复杂度： $O(k)$ $k$ 为整数的取值范围
- 最小时间复杂度： $O(N+k)$
- 平均时间复杂度： $O(N+k)$
- 最坏时间复杂度： $O(N+k)$

桶排序

简介
桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。
动图演示

代码实现，视数据而定（稳定排序）

# 示例
def bucket_sort(nums):
    bucket = [[] for i in range(10)]
    for i in nums:
        bucket[int(10*i)].append(i)
    output = []
    for b in bucket:
        output.extend(sorted(b))
    return output
from random import random
nums = [random() for _ in range(20)]
bucket_sort(nums)

算法复杂度
- 空间复杂度： $O(n+k)$ $k$ 为桶的数目
- 最小时间复杂度： $O(N+k)$
- 平均时间复杂度： $O(N)$
- 最坏时间复杂度： $O(N^2)$

基数排序

简介
基数排序是一种非比较型整数排序算法，其原理是将数据按位数切割成不同的数字，然后按每个位数分别比较。
假设说，我们要对 100 万个手机号码进行排序，应该选择什么排序算法呢？排的快的有归并、快排时间复杂度是 O(nlogn)，计数排序和桶排序虽然更快一些，但是手机号码位数是11位，那得需要多少桶？~~内存条表示不服~~。这个时候，我们使用基数排序是最好的选择。
动图演示

代码实现，类似桶排序，稳定排序

# 按十进制
def radix_sort(nums):
    if not len(nums):return nums
    ma = max(nums) # 最大数字
    n,radix = len(str(ma)),10 # 十进制
    for i in range(n):
        bucket = [[] for _ in range(radix)]
        for num in nums:
            bucket[(num//radix**i)%radix].append(num)
        nums = []
        for b in bucket:
            nums.extend(b)
    return nums