文章设置了主页隐藏,内容可能不完整,正在撰写中。。。
唠唠闲话
问题背景
去年讨论班,为了理解 Becker 文章 提到的图自同构子群,对仿射 Weyl 群的几何性质做了整理探究。

关于图自同构
定义及性质:
-
令 Φfin 为有限型根系,其单根系选取不唯一,取 Πfin 为其中一个单根系。
-
Weyl 群 Wfin 元素诱导单根系之间的置换,其自然作成 Aut(Φfin) 子群,且有
wΠfin=w′Πfin⇔w=w′
-
令 Γfin 为根系 Πfin 的自同构群,则其自然作成 Aut(Φfin) 的子群,且有
Aut(Φfin)≅Wfin⋊Γfin
-
具体地,图自同构有如下计算方法
⇒ ⇒ ⇒ σ∈Aut(Φfin)σΠfin=Π′=wΠfin, ∃ w∈Wfinw−1σΠfin=Πfinw−1σ∈Γfin
-
图自同构是单根间的置换,在 Dynkin 图上体现为图的自同构。从半直积关系可以看出,Γfin 作为 Aut(Φfin) 的子群,选取不唯一,与单根系选取相对应。
Ps:当讨论涉及根格,三角分解和 Verma 模等时,都隐含了单根系的选取,此时 Γfin 唯一确定。
文献结论
Bourbaki 文献 [B] 的 5.2.3 给出了下边关系
LetGWeWaffthenG/WeWe/WaffG/Waff=Aut(Φfin)⋉P∨=Wfin⋉P∨=Wfin⋉Q∨≅Aut(Φfin)/Wfin≅Γfin ≅P∨/Q∨≅Γ′≅(Aut(Φfin)/Wfin)⋉(P∨/Q∨)≅Γfin⋉Γ′≅Γ(1)(2)(3)
记号如下:
- We 为扩张仿射 Weyl 群
- Waff 为仿射 Weyl 群
- Wfin 为有限型的 Weyl 群
- Aut(Φfin) 为有限型根系的自同构群
- P∨, Q∨ 分别为权格对偶和根格对偶
- Γ 为仿射型的图自同构群
- Γfin 为有限型的图自同构群
其中 Γ′ 为 Becker 文献中提到的图自同构子群
探究结论
特别地,
WeΓ′≅Waff⋊Γ′≅Wfin⋉P∨≅(Wfin⋉Q∨)⋊Γ′≅P∨/Q∨
Γ′ 的元素唯一分解为平移变换 x 和线性变换 w:
∀ σ∈Γ′, ∃! x∈P∨∖Q∨, w∈Wfin s.t. σ=w⋅tx
考虑下边表格:
| 仿射型 GCM Aaff |
Al |
Bl |
Cl |
Dl |
E6 |
E7 |
E8 |
F4 |
G2 |
| 有限型 GCM Afin |
Al |
Bl |
Cl |
Dl |
E6 |
E7 |
E8 |
F4 |
G2 |
| 仿射型图同构群 Γaff |
D2(l+1) |
Z2 |
Z2 |
{Z4⋊Z2,S4,l>4l=14 |
S3 |
Z2 |
1 |
1 |
1 |
| 有限型图同构群 Γfin |
{1,Z2,l=1l>1 |
1 |
1 |
{Z2,S3,l>4l=4 |
Z2 |
1 |
1 |
1 |
1 |
| 图同构子群 Γ′≅P∨/Q∨ |
Zl+1 |
Z2 |
Z2 |
{Z4,Z2×Z2,l is oddl is even |
Z3 |
Z2 |
1 |
1 |
1 |
由最后一行知:
- 情形 F2,G2 和 E8 :图同构子群 Γ′ 为平凡群;
- 情形 D2k : Γ′≅K4 由两个元素生成
- 余下情形: Γ′ 为非平凡循环群
令 {ωi}i=1n 为有限型的基本权,相关公式的构造如下:
TypeAlBl(l≥3)Cl(l≥2)Dl(l为奇数)Dl(l为偶数)E6E7平移 xhωl=l+11i=1∑lihihω1=21hl+i=1∑l−1hihωl=21i=1∑lihihωl=21i=1∑l−2ihi+41((l−2)hl−1+lhlhωl, hωl−1−hωl=21(hl−1−hl)hω6=31(2h1+3h2+4h4+6h4+5h5+4h6)hω7=21(2h1+3h2+4h4+6h4+5h5+4h6+3h7)Weyl 群元素 wslsl−1⋯s1s1s2⋯sl−1slsl−1⋯s1w1w2⋯wlw1−w2+⋯wl−1+w1−w2+⋯wl−1−,w2+s0s1⋯sl−1w1s4s3s5s4s2w3s1w1s4s3s5s4s2s6s5s4s3s1w2s4s5s6s7
其中
wiwi+wi−=slsl−1⋯s1=sl−1sl−2⋯si=slsl−2sl−3⋯si
公式思路
平移部分:
- 图自同构 ⇔ 单根自同构 ⇔ alcove 的自同构(几何)
- 平移要用 alcove 的顶点,恰好为基本权 {ωi}i=1n
- D2k 情形取了 x=hωl−1−hωl,因而 Weyl 群公式带 s0
Weyl 群部分:
- 观察图像,得 A2 公式 s2s1,并证明一般情形 slsl−1⋯s1
- 遍历低阶 weyl 群,得出各类型的公式;公式可证,但说明不了简约性,此外群阶为 O(n!)
- 借助偏序给出升链算法,简约性立得,且复杂度至多 O(n3)(手算级别)
- 表达式含义:抛物子群最小陪集的最长元
Ps:结构越丰富,性质越好证。
内容安排
本篇整理 Weyl 群几何直观的相关结论,研究目的:
- 理解几何结构,有利于公式推导和证明,也利于编程
- 上周南大报告讲 Weyl groupoids 的几何直观,空间剖分方式和 Weyl 群很类似。李理论的理解清楚了,方便类比到 Nicholas 代数。
文章安排
- 根空间剖分与反射群的组合性质
- 有限型的推广方法
- 沿用原来方法
- 取对偶空间(Humphreys 5.13)
- 先补维再模维(GCM)
- 尝试:编程猜想+编程证明
反射群
定义记号
-
基本定义 (Π,S,W,Φ,V)
- Π={αi}i=1n 为单根系
- S={si}i=1n 为单反射集
- W=⟨s∣s∈S⟩ 为反射群
- Φ=WΠ 为根系
- V=spanΠ 为根空间
-
令 I⊆S 为单反射子集,得到子结构
(ΠI,I,WI,ΦI,VI)
其中 WI=⟨s∣s∈I⟩ 称为 W 的抛物子群。
-
长度函数记为 l,简约表达(略)。
-
WI 的最小(左)陪集定义为
WI:=={w∈W∣l(w)≤l(ws), ∀s∈I}{w∈W∣l(w)≤l(u),∀u∈wWI}
-
容易得到
l(u⋅v)=l(u)+l(v), ∀ u∈WI, v∈WI
几何性质
基本定义:
- 记 ⟨,⟩ 为 V 上的內积,α∈Φ
- Lα={λ∈V∣⟨λ,α⟩=0} 为墙
- Uα={λ∈V∣⟨λ,α⟩>0} 为半平面
- C=α∈Π⋂Uα 为基本室(fundamental chamber)
- D=Cˉ=α∈Π⋂(Uα∪Lα) 为基本区域
A2 例子:
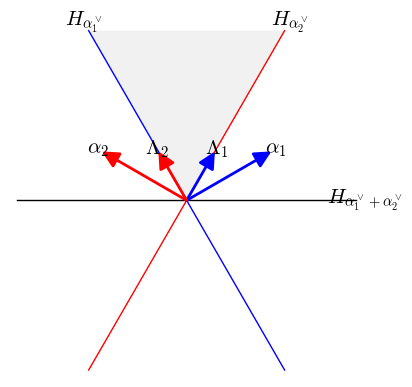
∀ λ,μ∈V ,定义偏序关系
λ≥μ⇔λ−μ=i=1∑nkiαi, where ki∈R≥0
特别地,考虑单反射 si 作用,λ 与 siλ 必有大小关系
siλ−λ=⟨αi,αi⟩2⟨αi,λ⟩αi
子结构
考虑子结构 (ΠI,I,WI,ΦI,VI),令
CI:=={λ∈D∣⟨λ,α⟩=0, α∈ΠI, ⟨λ,α⟩>0, α∈Π∖ΠI}(α∈ΠI⋂Lα)∩(α∈Π∖ΠI⋂Uα)
我们称 CI 为“小面” facet,其上任一点的稳定子群为抛物子群 WI:
stab(x)=WI, ∀x∈CI
特别地,两种极端情形如下
Cϕ=C, Wϕ=WCS=0, WS=0
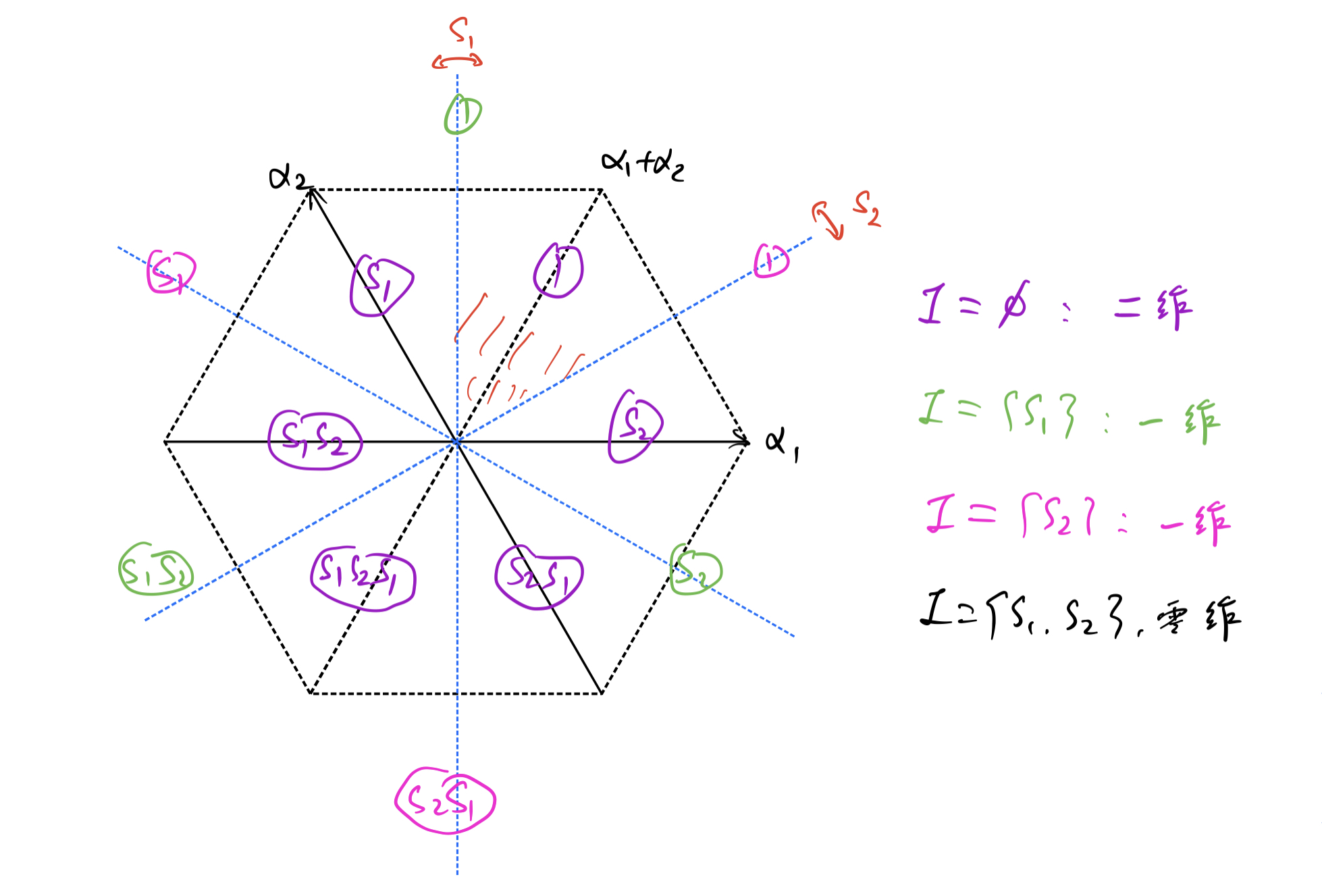
注记:
- 小面 CI 的“维数”越大,稳定子群 WI 越小,最小陪集 WI 相应越大。
- 小面公式 = 邻近大面中的最小公式
主要定理
-
抛物子群的最小陪集 WI 与 V 的小面一一对应
WI⟶{wCI∣w∈WI}
-
特别地,反射群与 V 的室(chamber)一一对应
W⟶{wC∣w∈W}
-
所有小面互不相交,作成空间 V 的剖分
V=I⊆S⋃.w∈WI⋃.wCI
-
引理:小面 CI 满足如下性质,用于构造升链
if x∈/CI,then ∃ si∈Π s.t. six>x
-
算法:∀ x∈V,借助升链给出 x 所在小面的表达式
- 设 WI=stab(x),则 x 落在 CI 的轨道上
- 取 x 的一条升链
x=x0→s1x1→s2⋯→skxk
- 由于反射群为有限群,不妨设升链取极大,此时 xk∈CI,继而
xksksk−1⋯s1x∈CI⇒ x∈s1s2⋯skCI
Ps:升链技巧出现在 Humphreys 1.12 引理的证明。
最长元公式
公式化归
考虑一般问题:∀ I⊆S,求 WI 的最长元公式。
- 若 I=S,则 WI=1,问题平凡
- 若 #(S∖I)>1,设 I⊂J⊂S
LetWWJthenWThusWI=WIWI=WJWJ=WI′WI=WJWJ=WJWI′WI=WJWI′
即 WI 的最长元公式拆分为两段。
- 综上,只需求 I=S∖{si} 情形的一般公式,通过拼凑得到任意抛物子群的最长元。
Ps:下一步化归非连通情形,最后归结为几组公式。
最长元的几何直观
- 设 w0 为反射群的最长元,容易证明 w0C=−C。
- 设 w0I 为最小陪集 WI 的最长元,则 w0ICI⊆−C,证明如下
Let w0then w0ICI=w0I⋅v∈ WIWI=w0IvCI=w0CI⊆−C
注记:
- −C 所有小面的表达式都是陪集最长元
- w0ICI 未必等于 −CI,比如 A2
- 当 −1∈W 时,必有 w0ICI=−CI
A2 例子

Coxeter 群
关于 GCM
直接推广
群作用空间的剖分技巧,取余维一的超空间,在平面跑动,分割,取法不唯一。取基本权,可以和根格权格建立联系,几何性质更好控制。(“坐标系”的选取)
按几何性质,不存在超平面产生仿射效果
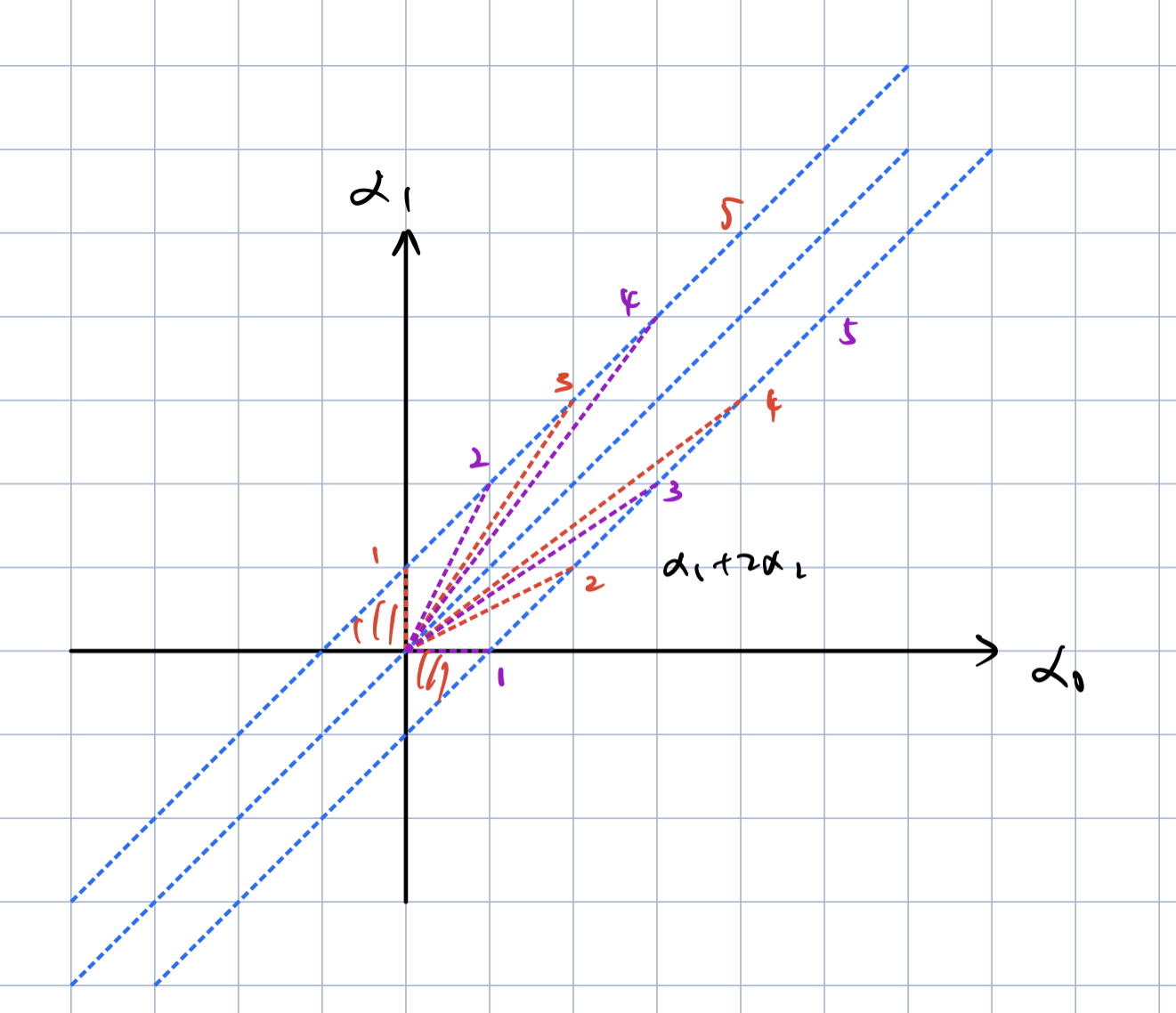
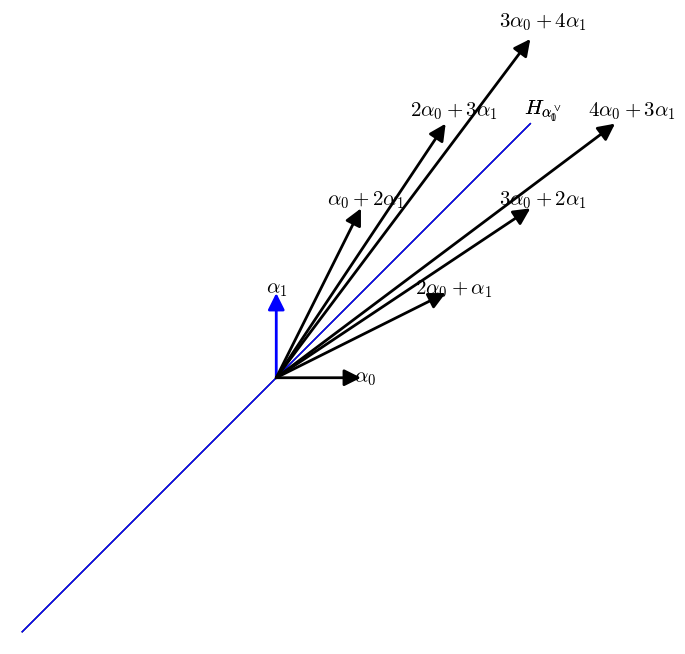
取对偶空间
取对偶空间上的几何
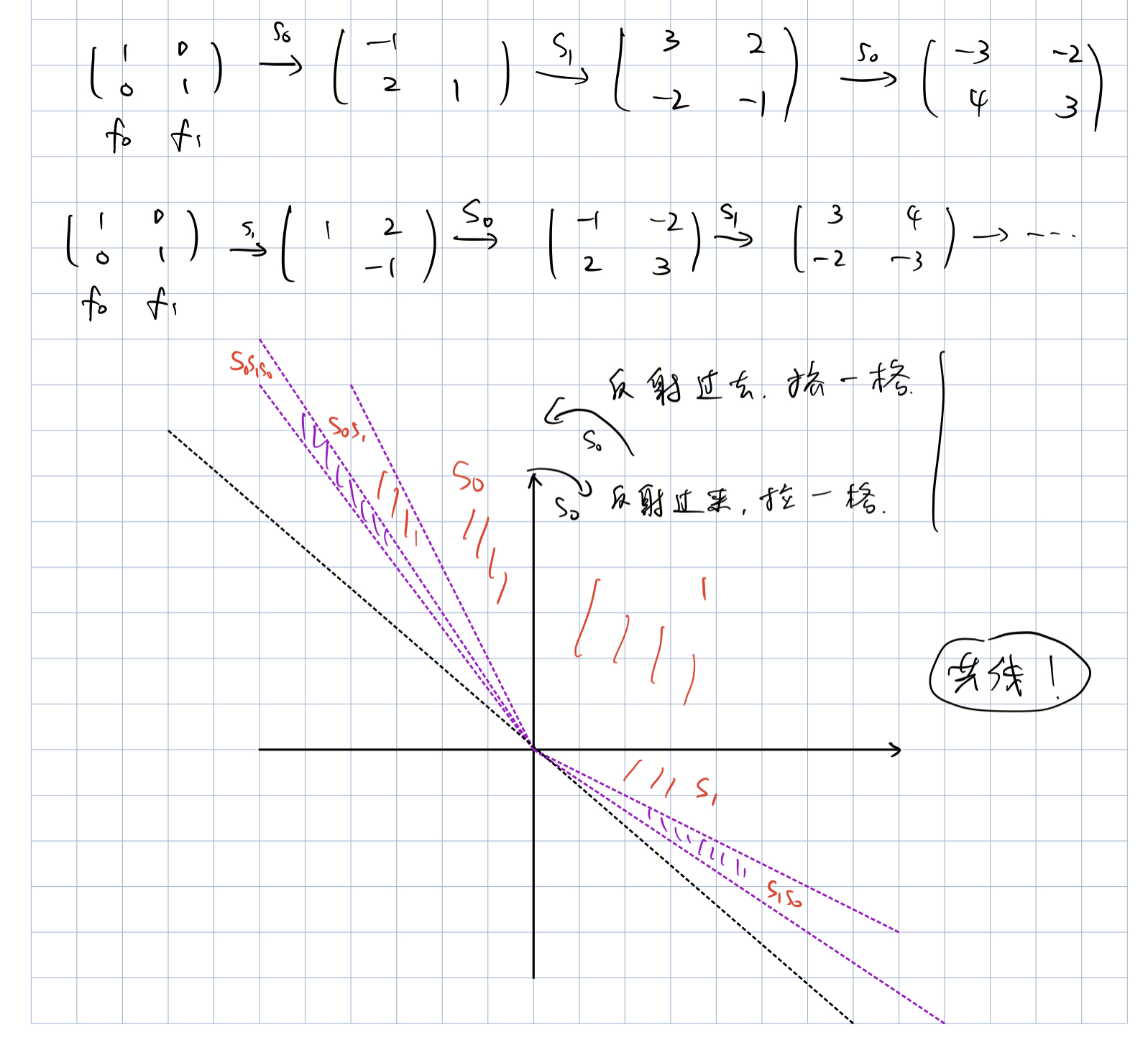
仿射 Weyl 群上的几何
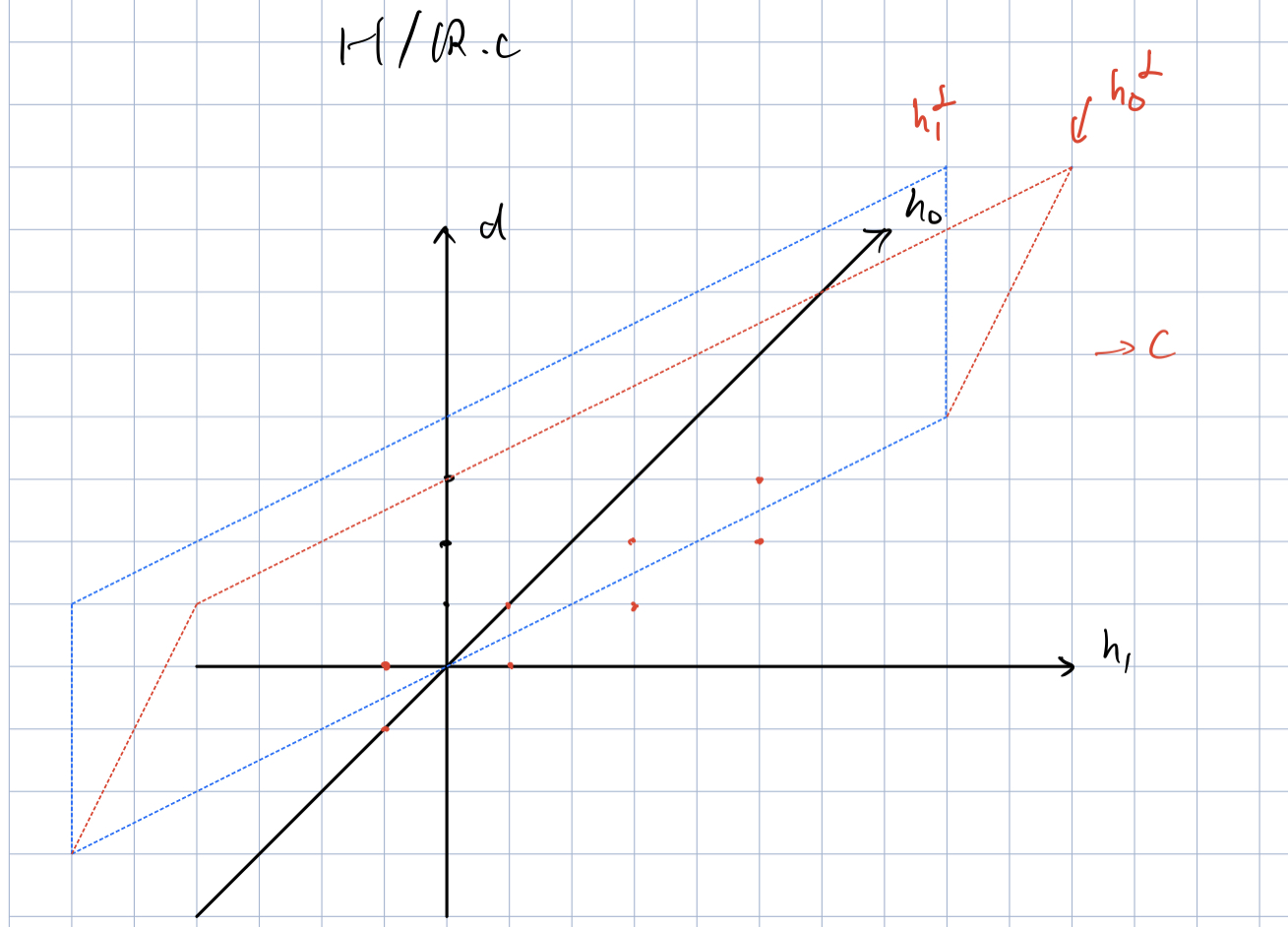
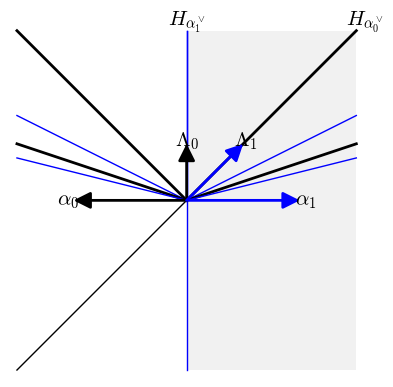
A3
编程尝试
(理论角度比较肤浅。)
拆两个函数,一个猜公式,一个证公式。
公式推导
考虑这个问题的好处:
验证公式在空间 H 上,分解称基元的线性组合。证明其实是对系数向量归纳(线性代数)。
交互式定理证明器 | Lean 简介












