唠唠闲话

同学项目里的一道问题，表述简单且不需要什么理论背景。

本篇介绍用 Python 写的处理这一问题的工具，内容如下：

二叉树问题
工具演示
算法及测试

附：代码 GitHub 地址

二叉树优化问题

下边涉及的二叉树都要求满足性质：每个节点要么有两个子节点，要么没有子节点。

给定二叉树，通过统计每行叶节点数目，得叶节点序列，如图
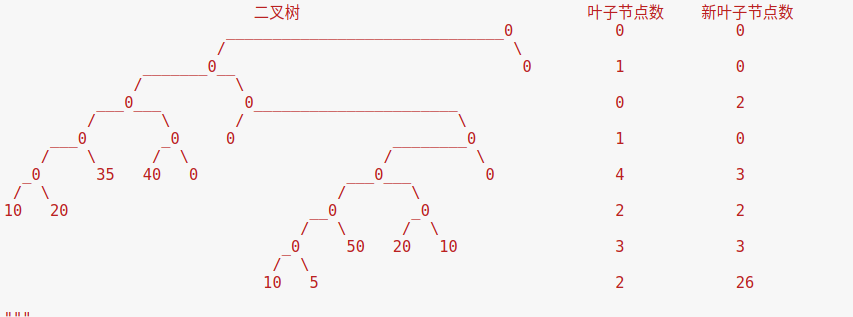
给定新的叶节点序列，对二叉树做以下操作，使叶子节点数满足新序列：
- 将节点与其所有子节点合并，操作开销为其子叶节点数值之和
- 将叶节点展开，操作开销为叶节点的数值
求满足要求的最小开销和操作。

使用演示

下载仓库，在目录下运行 Python

1	git clone git@github.com:RexWzh/binary_tree.git

示例

导入模块
1
from btree import *

输入初始树和叶节点信息

n = 8
positions = [None for i in range(2**n-1)] # 旧树
pos = [1, 2,3, 4,5, 8,9,10,11, 16,17,18,19,22, 23,32,33,44,45, 88,89,90,91, 176,177]
value = [0, 0,0, 0,0, 0,0,0,0, 0,35,40,0,0, 0,10,20,0,0, 0,50,20,10, 10,5]
for p,v in zip(pos,value):
    positions[p-1] = v
leaves = [0,0,2,0,3,2,3,26]

运行主函数 main，并打印计算结果

optimal,cost = main(positions,leaves)
print("操作开销",cost)
old = list_to_tree(positions)
sep,com = get_operations(old,optimal)
print("拆开位置",sep,"合并位置",com)

显示如下

1 2	操作开销 0 拆开位置 {19, 10, 3} 合并位置 set()

算法及测试

算法用 BFS 遍历， Python 编写，步骤参看 main 函数代码。

关键函数 next_level ：“树 -> 增加一层节点的树集” 。
next_level 工作内容：

获取 tree 的最后一层节点 last_layer
将节点分三类，优先展开(sep)，尽量不展开(not_sep)和随便(whatever)
从 last_layer 里取 ak 个节点展开，每种取法得一棵新树
利用三类节点信息，减少选取可能并记录开销
返回值：添加一层节点的新树，并判断是否已到最后一层

main 函数：

def main(positions,leaves):
    """函数打包"""
    n = len(leaves)
    old = list_to_tree(positions)
    nonleaf_cost,leaf_cost = get_nodes_cost(old) # 节点开销信息
    nonleaves = leaves_to_nonleaves(leaves)
    root = BTree(0)
    root.cost = 0 # 初始开销
    min_cost = sum(leaf_cost.values()) # 最小开销
    optimal = None # 最优解
    tmp_trees = [root] # 待遍历集合
    while len(tmp_trees):
        tree = tmp_trees[0] # 取最小开销树
        tmp_trees = tmp_trees[1:]
        news,is_end = next_level(tree,nonleaves,nonleaf_cost,leaf_cost)
        # 处理新树
        if is_end: # 树已完全展开
            for new in news:
                if new.cost < min_cost:
                    min_cost = new.cost
                    optimal = new
                    tmp_trees = [tree for tree in tmp_trees if tree.cost<= min_cost]
        else: # 树不完整
            tmp_trees.extend(news) # 加入新结果
            tmp_trees.sort(key=lambda x:x.cost-x.depth) # 排序
    return optimal,min_cost

随机测试

随机生成叶子序列，测试运行速度，初始树同上。

import time
t = time.time()
for i in range(1000):
    leaves = random_leaves_seq(n)
    optimal,cost = main(positions,leaves)
print("用时 %.3fs"%(time.time()-t))

计算 1000 个数据，用时 1.520s。速度较慢但还能接受。慢主要因为类编程占用更多内存，用类实现方便但过程比较绕。如果直接对列表操作可以加快，但这没必要了，因为算法本身也有缺陷。

坏情况测试

当初始树或叶子序列有一方性质好时，计算时间短。但如果初始树和序列都取到坏情况，运行就吃力了。

坏情形的初始树

1 2	n = 8 positions = [0](2(n-1)-1) + list(range(2*(n-1)))

配合性质稍差的叶子序列 [0, 1, 0, 0, 5, 2, 5, 6]

leaves = [0, 1, 0, 0, 5, 2, 5, 6] # 18 秒
t = time.time()
optimal,cost = main(positions,leaves)
print("计算用时 %.3fs"%(time.time()-t))
print("操作开销",cost)
old = list_to_tree(positions)
sep,com = get_operations(old,optimal)
print("拆开位置",sep,"合并位置",com)