量子计算系列：

唠唠闲话

量子系列第二篇，内容如下：

Bloch 球面与纯态
Bloch 球面的几何性质
Bloch 球与混合态

本篇介绍 Bloch 球及其性质，在 Nakahara 第三章的基础上，补充命题和推导。

纯态与 Bloch 球面

量子比特

经典比特的取值为 1 或 0，由二极管的通电断电实现。

量子比特的取值是二维复空间 $\mathbb{C}^2$ 上的单位向量，以 $\vert 0\rangle = \begin{pmatrix} 1\\ 0 \end{pmatrix}$ 和 $\vert 1\rangle = \begin{pmatrix} 0\\ 1 \end{pmatrix}$ 为一组基。
物理上，实现基元 $\vert 0\rangle$ 和 $\vert 1\rangle$ 有多种方案：

自旋为 $\frac 12$ 的粒子，比如电子或质子
- $\vert 0\rangle = \vert \uparrow\rangle$ 为上旋
- $\vert 1\rangle = \vert \downarrow\rangle$ 为下旋
偏振光子(polarized photon)
- $\vert 0\rangle$ 取竖直偏振的光子 $\vert \updownarrow\rangle$
- $\vert 1\rangle$ 取水平偏振的光子 $\vert \leftrightarrow\rangle$

注记：

量子比特用复向量定义，因而属于纯态；
自旋是粒子的内禀属性，自旋度为 $S$ 的粒子能提供 $d=2S+1$ 种正交的自旋状态，用于构造 $d$ 种状态叠加的粒子，但这类粒子的重要性还有待探索。
量子计算与经典计算在硬件实现上有本质的不同，后者处理离散的0-1，而前者处理向量空间。

Bloch 球面

回顾上篇，纯态 $\vert\psi\rangle$ 代表集合等价类

$\{e^{i\alpha}\vert\psi\rangle\mid \alpha\in\mathbb{R}\}$

我们给出代表元的标准形式，用以建立纯态与球面的对应。引理： $\mathbb{C}^2$ 中的纯态有如下标准形式

$\vert\psi(\theta,\phi)\rangle=\cos\frac{\theta}{2}\vert 0\rangle+e^{i\phi}\sin\frac{\theta}{2}\vert 1\rangle,\theta\in[0,\pi],\phi\in[0,2\pi]$

证明：
将代表元 $a\vert 0\rangle+b\vert 1\rangle\in\mathbb{C}^2$ 标准化：

不妨设系数 $a$ 为实数，否则调整幅角使 $e^{i\alpha}a$ 为实数；将系数 $b$ 拆成指数形式，代表元化
$a\vert 0\rangle+be^{i\alpha}\vert 1\rangle,\ a,b,\alpha\in\mathbb{R}$
由归一化条件 $a^2+b^2=1$ ，代表元化
$\cos\frac{\theta}{2}\vert 0\rangle+e^{i\phi}\sin\frac{\theta}{2}\vert 1\rangle,\theta\in[0,4\pi],\phi\in[0,2\pi]$
夹角取 $\frac{\theta}{2}$ 方便与球面建立对应。
将 $\theta$ 取值范围缩小为 $[0,2\pi]$ ，当 $\theta>2\pi$ 时，如下变量代换
$\begin{align*} \cos\frac{\theta}{2}\vert 0\rangle+e^{i\phi}\sin\frac{\theta}{2}\vert 1\rangle =&-\left(\cos\frac{\theta-2\pi}{2}\vert 0\rangle+e^{i\phi}\sin\frac{\theta-2\pi}{2}\vert 1\rangle\right)\\ =&-\left(\cos\frac{\theta'}{2}\vert 0\rangle + e^{i\phi}\sin\frac{\theta'}{2}\vert 1\rangle\right)\\ where\quad \theta'=\theta-2\pi\in[0,2\pi] \end{align*}$
将 $\theta$ 取值范围缩小为 $[0,\pi]$ ，当 $\theta>\pi$ 时，如下变量代换
$\begin{align*} \cos\frac{\theta+\pi}{2}\vert 0\rangle+e^{i\phi}\sin\frac{\theta+\pi}{2}\vert 1\rangle =&-\cos(\frac{\pi}{2}-\frac{\theta}{2})\vert 0\rangle + e^{i\phi}\sin(\frac{\pi}{2}-\frac{\theta}{2})\vert 1\rangle\\ =&-\left(\cos\frac{\theta'}{2}\vert 0\rangle + e^{i(\phi+\pi)}\sin\frac{\theta'}{2}\vert 1\rangle\right)\\ where\quad \theta'=\pi-\theta\in[0,\pi] \end{align*}$

现在，对比二维球面 $S^2$ 与纯态标准形式

$S^2 = \{\vec{n}(\theta,\phi)=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)^t:\theta\in[0,\pi],\phi\in[0,2\pi]\}\\ \vert\psi(\theta,\phi)\rangle=\cos\frac{\theta}{2}\vert 0\rangle+e^{i\phi}\sin\frac{\theta}{2}\vert 1\rangle,\theta\in[0,\pi],\phi\in[0,2\pi]$

二者参数 $\theta$ 和 $\phi$ 的取值范围相同，且易证

$\vec{n}(\theta_1,\phi_1)=\vec{n}(\theta_2,\phi_2)\Leftrightarrow\vert\psi(\theta_1,\phi_1)\rangle=\vert\psi(\theta_2,\phi_2)\rangle$

于是 $\mathbb{C}^2$ 纯态与二维球面 $S^2$ 借由 $(\theta,\phi)$ 建立一一对应。

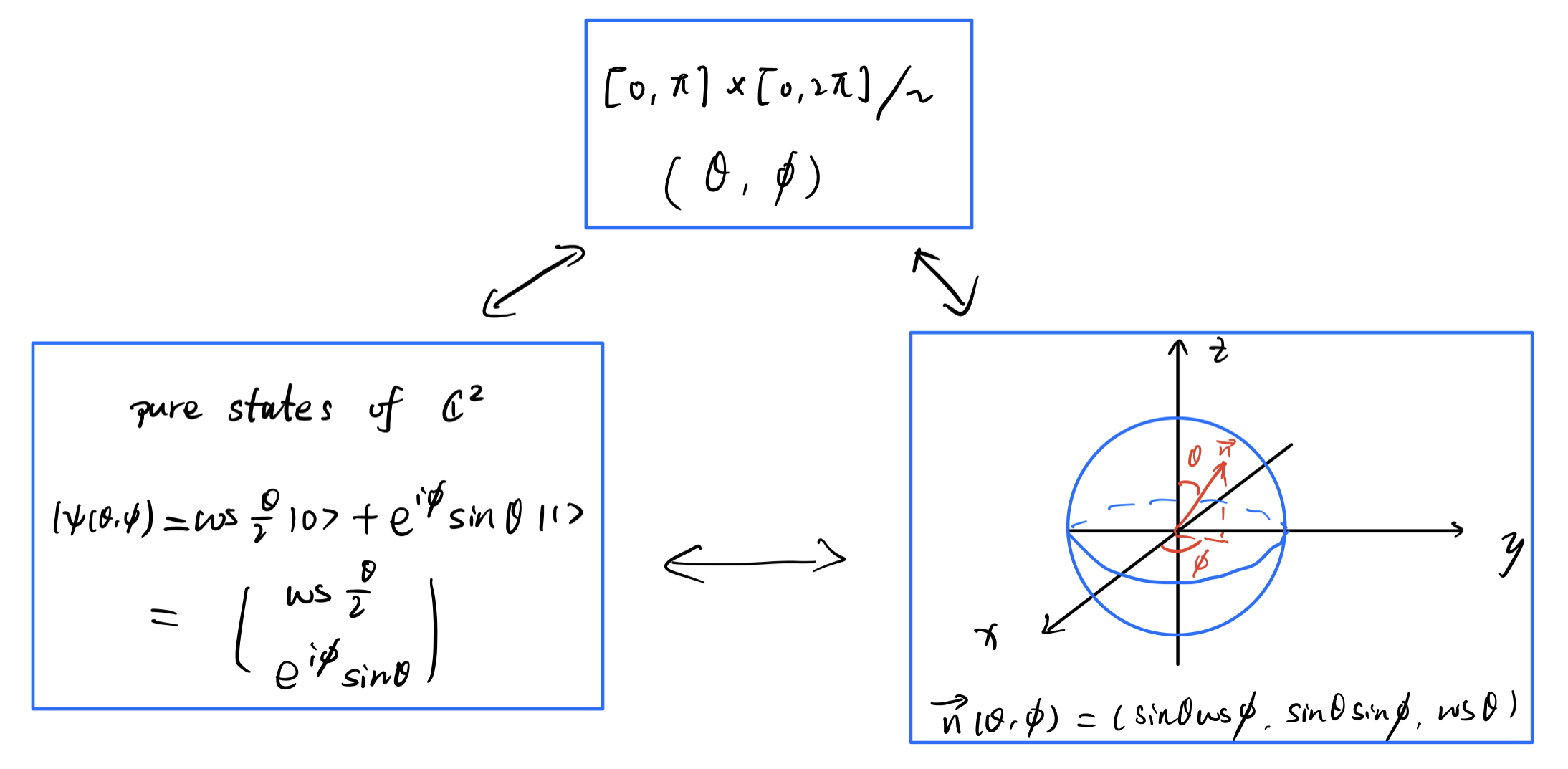
2021-10-23_19-31-53

我们称 $S^2$ 为 Bloch 球面，称向量 $\vec{n}(\theta,\phi)$ 为量子态 $\vert\psi(\theta,\phi)\rangle$ 的 Bloch 向量。

$\mathbb{C}^2$ 纯态构成二维曲面的一种理解：

从实数域看， $\vert\psi\rangle\in\mathbb{C}^2$ 是四维空间 $\mathbb{R}^4$ 上的向量，有 4 个自由变量；

由归一化条件 $\langle\psi\vert\psi\rangle=1$ ， $\psi$ 的自由变量剩 3 个；

再由整体相位 $e^{i\alpha}$ ，自由变量剩 2 个，得到二维球面 $S^2$ 。

$\mathbb{C}^2$ 是维数最低的量子系统，恰好能用 Bloch 球理解其量子态，但更高维的量子系统就很难再找到这种对应了。

几何性质

量子态 $\vert\psi\rangle$ 是复空间 $\mathbb{C}^2$ 中的向量，从实数域上看， $\mathbb{C}^2$ 是个四维空间，我们很难想象。但借助 $\mathbb{C}^2$ 纯态与二维球面 $S^2$ 的对应，我们可以用 Bloch 球面的几何性质理解 $\mathbb{C}^2$ 中纯态的几何性质。

下边探讨二者几何性质的联系，并导出泡利矩阵。

坐标轴

如下建立直角坐标系

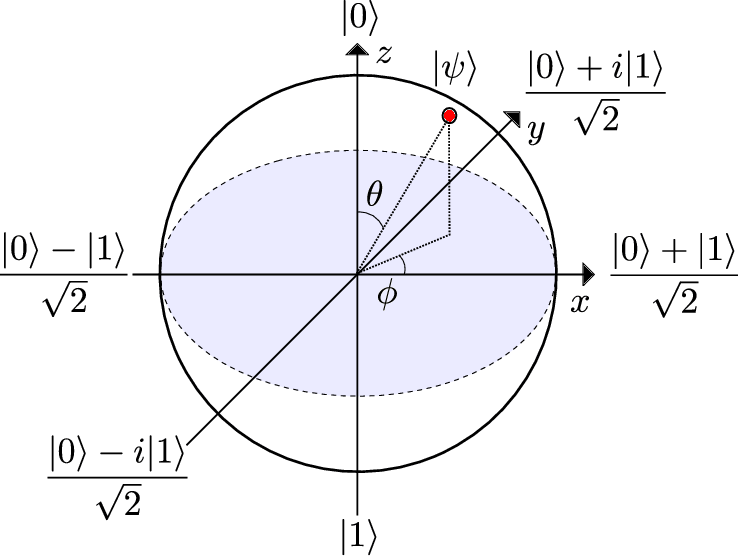
坐标轴的量子态与狄拉克记号：：

狄拉克符号	坐标轴方向	$S^2$ 坐标	$(\theta,\phi)$	量子态
$\vert 0\rangle$	$z^+$	$(0,0,1)$	$(0,0)$	$\vert 0\rangle=\begin{pmatrix}1\\ 0\end{pmatrix}$
$\vert 1\rangle$	$z^-$	$(0,0,-1)$	$(\pi,0)$	$\vert 1\rangle=\begin{pmatrix}0\\ 1\end{pmatrix}$
$\vert +\rangle$	$x^+$	$(1,0,0)$	$(\frac{\pi}{2},0)$	$\frac{\vert 0\rangle+\vert 1\rangle}{\sqrt{2}}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\ 1\end{pmatrix}$
$\vert -\rangle$	$x^-$	$(-1,0,0)$	$(\frac{\pi}{2},\pi)$	$\frac{\vert 0\rangle-\vert 1\rangle}{\sqrt{2}}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\ -1\end{pmatrix}$
$\vert +i\rangle$	$y^+$	$(0,1,0)$	$(\frac{\pi}{2},\frac{\pi}{2})$	$\frac{\vert 0\rangle+i\vert 1\rangle}{\sqrt{2}}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\ i\end{pmatrix}$
$\vert -i\rangle$	$y^-$	$(0,-1,0)$	$(\frac{\pi}{2},\frac{3\pi}{2})$	$\frac{\vert 0\rangle-i\vert 1\rangle}{\sqrt{2}}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\ -i\end{pmatrix}$

正交与反向

正交的量子态对应方向相反的 Bloch 向量：

$\langle\psi(\theta_2,\phi_2)\vert\psi(\theta_1,\phi_1)\rangle=0\Leftrightarrow \vec{n}(\theta_1,\phi_1)=-\vec{n}(\theta_2,\phi_2)$

证明：
令 $\alpha^+=\vec{n}(\theta,\phi),\alpha^-=\vec{n}(\pi-\theta,\pi+\phi)$ 为方向相反的两个向量，计算內积得

$\begin{align*} \langle\alpha^+\vert\alpha^-\rangle &= \langle\psi(\theta,\phi)\vert\psi(\pi-\theta,\pi+\phi)\rangle\\ &=\begin{pmatrix}\cos\frac{\theta}{2}& e^{-i\phi}\sin\frac{\theta}{2}\end{pmatrix}\begin{pmatrix}\cos\frac{\pi-\theta}{2}\\ e^{i(\phi+\pi)}\sin\frac{\pi-\theta}{2}\end{pmatrix}\\ &=\begin{pmatrix}\cos\frac{\theta}{2}& e^{-i\phi}\sin\frac{\theta}{2}\end{pmatrix}\begin{pmatrix}\sin\frac{\theta}{2}\\ -e^{i\phi}\cos\frac{\theta}{2}\end{pmatrix}\\ &=0 \end{align*}$

推论：量子态 $\vert\alpha^+\rangle$ 和 $\vert\alpha^-\rangle$ 作成 $\mathbb{C}^2$ 的一组正交基。

球投影算子

对向量 $\alpha^+=\vec{n}(\theta,\phi)\in S^2$ ，定义球投影算子

$\begin{align*} \sigma_{\alpha^+} &= \vert\alpha^+\rangle\langle\alpha^+\vert -\vert\alpha^-\rangle\langle\alpha^-\vert\\ &=\begin{pmatrix}\cos\frac{\theta}{2}\\ e^{i\phi}\sin\frac{\theta}{2}\end{pmatrix} \begin{pmatrix}\cos\frac{\theta}{2}& e^{-i\phi}\sin\frac{\theta}{2}\end{pmatrix} -\begin{pmatrix}\sin\frac{\theta}{2}\\ -e^{i\phi}\cos\frac{\theta}{2}\end{pmatrix} \begin{pmatrix}\sin\frac{\theta}{2}& -e^{-i\phi}\cos\frac{\theta}{2}\end{pmatrix}\\ &=\begin{pmatrix} \cos\theta & e^{-i\phi}\sin\theta\\ e^{i\phi}\sin\theta & -\cos\theta \end{pmatrix} \end{align*}$

由定义知， $\vert\alpha^\pm\rangle$ 分别为 $\sigma_{\alpha^+}$ 的特征值 $\pm 1$ 的特征向量。测量上，算子 $\sigma_{\alpha^+}$ 对纯态 $\vert\psi'\rangle$ 的测量期望为 $\vert\psi'\rangle$ 的 Bloch 向量 $\vec n'$ 在 $\alpha^+=\vec{n}$ 方向的投影，即：

$\begin{align*} \langle\sigma_{\alpha^+}\rangle&=\langle\psi(\theta',\phi')\vert\sigma_{\alpha^+}\vert\psi(\theta',\phi')\rangle\\ &=\begin{pmatrix}\cos\frac{\theta'}{2}& e^{-i\phi'}\sin\frac{\theta'}{2}\end{pmatrix} \begin{pmatrix} \cos\theta & e^{-i\phi}\sin\theta\\ e^{i\phi}\sin\theta & -\cos\theta \end{pmatrix} \begin{pmatrix}\cos\frac{\theta'}{2}\\ e^{i\phi'}\sin\frac{\theta'}{2}\end{pmatrix} \\ &=\cos\theta\cos\theta'+\sin\theta\sin\phi\sin\theta'\sin\phi'+\sin\theta\cos\phi\sin\theta'\cos\phi'\\ &=\vec n(\theta',\phi')\cdot\vec{n}(\theta,\phi) \end{align*}$

Ps：为不引起歧义，我们称 $\sigma_{\alpha^+}$ 为球投影算子，相对 Bloch 球的几何而言，注意与量子态的投影算子 $P_{\alpha^+}$ 区分：

$\begin{align*} \sigma_{\alpha^+} &=\vert\alpha^+\rangle\langle\alpha^+\vert-\vert\alpha^-\rangle\langle\alpha^-\vert\\ P_{\alpha^+}&=\vert\alpha^+\rangle\langle\alpha^+\vert \end{align*}$

泡利矩阵

特别地，将坐标轴正方向的球投影算子 $\sigma_x,\sigma_y,\sigma_z$ 称为泡利矩阵，由定义得，泡利矩阵 $\sigma_z$

$\begin{align*} \sigma_z&=\vert 0\rangle\langle 0\vert-\vert 1\rangle\langle 1\vert\\ &=\begin{pmatrix}1\\ 0\end{pmatrix} \begin{pmatrix}1& 0\end{pmatrix} - \begin{pmatrix}0\\ 1\end{pmatrix} \begin{pmatrix}0& 1\end{pmatrix}\\ &=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \end{align*}$

同理可求得 $\sigma_x$ 和 $\sigma_y$ 为

$\sigma_x = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix},\ \sigma_y = \begin{pmatrix} 0 & -i\\ i & 0 \end{pmatrix}$

纯态 $\vert\psi\rangle$ 的 Bloch 向量可由泡利矩阵量得到

$\vec{n} = (\langle\sigma_x\rangle,\langle\sigma_y\rangle,\langle\sigma_z\rangle)$

其中 $\langle\sigma_x\rangle,\langle\sigma_y\rangle,\langle\sigma_z\rangle$ 为 $\vert\psi\rangle$ 的测量期望。

直觉上，泡利矩阵提供物理量子系统 $\mathbb{C}^2$ 的坐标系。
实际上，记 $\vec\sigma=(\sigma_x,\sigma_y,\sigma_z)$ ，则有

$\begin{align*} \sigma_{\alpha^+} &= \begin{pmatrix} \cos\theta & e^{-i\phi}\sin\theta\\ e^{i\phi}\sin\theta & -\cos\theta \end{pmatrix}\\ &= \begin{pmatrix} \cos\theta & (\cos\phi-i\sin\phi)\sin\theta\\ (\cos\phi+i\sin\phi)\sin\theta & -\cos\theta \end{pmatrix}\\ &=\sin\theta\cos\phi\cdot\sigma_x + \sin\theta\sin\phi\cdot\sigma_y+\cos\theta\cdot\sigma_z\\ &=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)\cdot(\sigma_x,\sigma_y,\sigma_z)\\ &=\vec{n}(\theta,\phi)\cdot\vec\sigma \end{align*}$

向量 $\vec{n}$ 与 $\vec\sigma$ 点积，得到 $\vec n$ 方向的球投影算子 $\sigma_{\alpha^+}$ 。

混合态与 Bloch 球

$\mathbb{C}^2$ 的量子态与 Bloch 球的向量一一对应，其中纯态对应 Bloch 球面，混合态对应 Bloch 球内点，下边通过“坐标分解”建立这一对应。

坐标分解

回顾上篇：

混合态用密度矩阵 $\rho$ 表示
$\mathcal{H}$ 上的密度矩阵全体记为 $\mathcal{S}(\mathcal{H})$
$\mathcal{S}(\mathcal{H})$ 与量子态一一对应，其中秩为 1 的部分对应纯态
密度矩阵 $\rho$ $ρ$ 由下边三条性质等价刻画：
1. $\rho^\dagger=\rho$
2. $\rho$ 为半正定矩阵
3. $Tr(\rho)=1$

借助泡利矩阵，我们给出密度矩阵 $\rho\in\mathcal{S}(\mathbb{C}^2)$ 的坐标分解：

记 $I=\begin{pmatrix}1 & 0\\ 0 & 1\end{pmatrix}$ 为单位矩阵，则 $\{I,\sigma_x,\sigma_y,\sigma_z\}$ 作成 $End_\mathbb{C}(\mathcal{H})$ 的一组基元，设：
$\rho=b_x\sigma_x+b_y\sigma_y+b_z\sigma_z+b_0I,\quad b_x,b_y,b_z,b_0\in\mathbb{C}$
断言 $b_x,b_y,b_z,b_0$ 为实数，由于
$\begin{align*} &\rho^\dagger=\rho \\ \Rightarrow &\ b_x\sigma_x+b_y\sigma_y+b_z\sigma_z+b_0I = b_x^*\sigma_x+b_y^*\sigma_y+b_z^*\sigma_z+b_0^*I\\ \Rightarrow &\ (b_x-b_x^*)\sigma_x+(b_y-b_y^*)\sigma_y+(b_z-b_z^*)\sigma_z+(b_0-b_0^*)I = 0\\ \Rightarrow &\ b_x-b_x^*=b_y-b_y^*=b_z-b_z^*=b_0-b_0^*=0 \end{align*}$
由 $Tr(\rho)=1$ 得 $b_0=\frac{1}{2}$ ，将 $\rho$ 写为如下形式
$\begin{align*} \rho&=\frac 12(a_x\sigma_x+a_y\sigma_y+a_z\sigma_z+I)\\ &=\frac 12\left((a_x,a_y,a_z)\cdot \vec{\sigma}+ I\right)\\ &=\frac 12\left(\vec{n}\cdot \vec{\sigma}+ I\right),\quad \vec{n}\in \mathbb{R}^3 \end{align*}$
易见 $\vec{n}\cdot\vec\sigma$ 的特征值为 $\pm\Vert \vec{n}\Vert$ ，进而 $\rho$ 的特征值为 $\frac{\pm\Vert \vec{n}\Vert+1}{2}$ ，再由 $\rho$ 的半正定性，得
$\frac{\pm\Vert \vec{n}\Vert+1}2\geq0,\ i.e.\ \Vert\vec{n}\Vert\leq 1$

综上，密度矩阵标准形式为

$\rho=\frac 12\left(\vec{n}\cdot \vec{\sigma}+ I\right),\quad \vec{n}\in \mathbb{B}^3$

其中 $\mathbb{B}^3$ 为三维空间的单位球。
反之，易见上述形式给出的 $\rho$ 为密度矩阵，于是建立对应关系：

$\begin{align*} \mathcal{S}(\mathbb{C}^2)&\overset{\sim}{\longrightarrow}\mathbb{B}^3\\ \rho=\frac 12\left(\vec{n}\cdot \vec{\sigma}+ I\right)&\longmapsto \vec n \end{align*}$

定义相容性

前边将纯态 $\vert\psi\rangle$ 与 Bloch 球面建立对应；注意到纯态也可以通过密度矩阵建立和 Bloch 球的对应，下边式子说明两种方式得到同一对应。

$\begin{align*} &\vert\psi(\theta,\phi)\rangle=\begin{pmatrix}\cos\frac{\theta}{2}\\ e^{i\phi}\sin\frac{\theta}{2}\end{pmatrix} \\ &\rho = \vert\psi\rangle\langle\psi\vert=\begin{pmatrix}\cos\frac{\theta}{2}\\ e^{i\phi}\sin\frac{\theta}{2}\end{pmatrix}\begin{pmatrix}\cos\frac{\theta}{2}& e^{-i\phi}\sin\frac{\theta}{2}\end{pmatrix}\\ &\ \ =\begin{pmatrix} \frac{\cos\theta+1}{2} & e^{-i\phi}\frac{\sin\theta}2\\ e^{i\phi}\frac{\sin\theta}2 & \frac{\cos\theta+1}{2} \end{pmatrix}\\ &\ \ =\frac 12\left(\vec{n}(\theta,\phi)\cdot \vec{\sigma}+ I\right) \end{align*}$

两种途径定义的 Bloch 向量都是

$\vec n(\theta,\phi) = (\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)$

此外，球投影算子 $\sigma_{\alpha^+}$ 对混合态的测量期望仍是 Bloch 向量在 $\alpha^+$ 方向上的投影。以 $\sigma_x$ 为例，由密度矩阵的测量公式，得

$\begin{align*} \langle\sigma_{x}\rangle&=Tr(\sigma_{x}\rho)\\ &=Tr\left(\frac 12\sigma_{x}\left(\vec{n}\cdot \vec{\sigma}+ I\right)\right)\\ &=Tr\left(\frac 12\sigma_{x}\left(a_x\sigma_x+a_y\sigma_y+a_z\sigma_z+ I\right)\right)\\ &=Tr\left(\frac 12\left(a_xI+ia_y\sigma_z-ia_z\sigma_y+ \sigma_x\right)\right)\\ &=Tr(\frac{a_x}2I)=a_x \end{align*}$

$a_x$ 为 Bloch 向量 $\vec{n}$ 的 x 轴坐标，也即 $\vec n$ 在 x 轴方向上的投影。

谱分解与完全混合态

下边从量子态和 Bloch 球两个角度，理解密度矩阵的谱分解和完全混合态。

从 $\mathcal{S}(\mathcal{H})$ 上看

凸线性组合
称 $x=\sum\limits_{i=1}^r\lambda_ix_i$ 为向量集 $\{x_i\}_{i=1}^r$ 的一个凸线性组合，若 $\lambda_i\geq 0$ 且 $\sum\limits_{i=1}^r\lambda_i=1$ 。
易见密度矩阵的凸线性组合仍是密度矩阵。
密度矩阵为正规矩阵，做谱分解

$\begin{align*} \rho&=\sum_{i=1}^r \lambda_i\vert\lambda_i\rangle\langle\lambda_i\vert\\ &=\sum_{i=1}^r\lambda_i\rho_i \end{align*}$

其中 $\rho_i=\vert\lambda_i\rangle\langle\lambda_i\vert$ 为纯态的密度矩阵， $\rho$ 为纯态 $\{\rho_i\}_{i=1}^r$ 的凸线性组合。一般来说，纯态 $\rho_i$ 的取法不唯一。
考虑 $\rho\in\mathcal{S}(\mathbb{C}^2)$ ，此时 $\rho=\lambda_1\rho_1+\lambda_2\rho_2$ ，由“不同特征值的特征向量线性无关”知：
- 当 $\rho\neq \frac 12I$ 时， $\rho_1$ 和 $\rho_2$ 唯一确定
- 当 $\rho = \frac 12I$ 时，必有 $\lambda_1=\lambda_2=\frac 12$ 且 $\rho_1$ 和 $\rho_2$ 可取任意两个正交态，此时称 $\rho$ 为完全混合态

从 Bloch 球上看

密度矩阵的凸线性组合，对应 Bloch 向量的凸线性组合

$\begin{align*} \rho_1&=\frac 12\left(\vec{n_1}\cdot \vec{\sigma}+ I\right)\\ \rho_2&=\frac 12\left(\vec{n_2}\cdot \vec{\sigma}+ I\right)\\ \Rightarrow\rho&=\lambda_1\rho_1+\lambda_2\rho_2\\ &=\frac 12\left((\lambda_1\vec{n_1}+\lambda_2\vec{n_2})\cdot \vec{\sigma}+ I\right)\\ \Rightarrow\vec n&=\lambda_1\vec{n_1}+\lambda_2\vec{n_2} \end{align*}$
从 Bloch 球 $\mathbb{B}^3$ 上看：
- 谱分解将 Bloch 向量 $\vec{n}$ 分解为方向相反的两个球面向量 $\vec{n}^-,\vec{n}^+$ （正交=反向，纯态=球面）
- 当 $\vec n\neq 0$ 时， $\vec{n}^-,\vec{n}^+$ 唯一确定，为 $\vec{n}$ 所在直线与 Bloch 球面的两个交点
- 当 $\vec n= 0$ 为 Bloch 球原点时， $\vec n$ 可分解为任意两个方向相反的球面向量，对应完全混合态

酉变换

回顾上篇，演化算子 $U$ 是酉算子，作用量子态上：

向量形式 $\vert\psi\rangle \rightarrow U\vert\psi\rangle$
密度矩阵形式 $\rho\rightarrow U\rho U^\dagger$

注意到球投影算子 $\sigma_{\alpha^+}$ 不仅满足 Hermitian 性质，还是个酉算子，因而可作用在量子态上。

从 Bloch 球上看， $\sigma_{\alpha^+}$ 的作用效果是将空间绕 x 轴旋转 $180\degree$ 。以 $\sigma_x$ 为例：

$\begin{align*} let\ \rho &= \frac 12\left(\vec{n}\cdot \vec{\sigma}+ I\right)\\ \sigma_x\rho\sigma_x^\dagger&=\frac 12\sigma_x\left(\vec{n}\cdot \vec{\sigma}+ I\right)\sigma_x\\ &=\frac 12\left(\vec{n}\cdot \sigma_x\vec{\sigma}\sigma_x+ I\right)\\ &=\frac 12\left((n_x,n_y,n_z)\cdot (\sigma_x,-\sigma_y,-\sigma_z)+ I\right)\\ &=\frac 12\left((n_x,-n_y,-n_z)\cdot \vec{\sigma}+ I\right)\\ (n_x,n_y,n_z)&\overset{rotate\ 180\degree}{\longrightarrow} (n_x,-n_y,-n_z) \end{align*}$

思考题： $\mathbb{C}^2$ 上既能当成测量，又能当成演化的算子有哪些？或者判断正误：

$\{\sigma_{\alpha^+}\mid\alpha^+\in S^2\}\overset{?}=\{\sigma\in End(\mathbb{C}^2)\mid \sigma=\sigma^\dagger=\sigma^{-1}\}$

Ps：本节提到了三类算子，注意区分

密度矩阵：Hermitian + 半正定 + 迹为 1

测量算子：Hermitian

演化算子：Unitary

$\sigma_{\alpha^+}$ ，视语境可能是测量算子，也可能是演化算子

$P_\alpha=\vert\alpha^+\rangle\langle\alpha^+\vert$ ，视语境可能是投影算子，也可能是纯态的密度矩阵

总结

本篇建立 $\mathbb{C}^2$ 量子态与 Bloch 球的对应，通过 Bloch 球的几何性质理解量子态，主要内容：

量子比特 $\vert 0\rangle$ 和 $\vert 1\rangle$
纯态 $\vert\psi\rangle$ 标准化，与 Bloch 球面建立对应
正交的量子态对应 Bloch 球面方向相反的向量，导出“球投影算子”
球投影算子导出泡利矩阵，提供量子系统的“坐标系”
借助泡利矩阵，将密度矩阵做“坐标分解”，建立与 Bloch 球的对应
进一步讨论：谱分解，完全混合态，测量 + 酉变换

关于 Bloch 球

Bloch 球只能表示 $\mathbb{C}^2$ 的量子态，更高维数的量子系统很难找到类似 Bloch 球这样精巧的对应。
$\mathbb{C}^{2^n}$ 的分离态可用多个 Bloch 球表示。因此一些特殊的量子门，比如 Walsh-Hadamard 门和量子傅里叶变换，其作用在分离态后仍得到分离态，可用 Bloch 球演示变化过程。
对一般的量子门，如果将分离态变换为纠缠态，就无法用 Bloch 球演示了。

拓展-MUB 问题

Bloch 球的几何直观可用于解决一些难题，比如清华视频课里提到的 MUB 问题(Mutually unbiased bases)：

称希尔伯特空间 $\mathcal{H_d}=\mathbb{C}^d$ 的两组标准正交基 $\{\vert\psi_i\rangle\}_{i=1}^d,\{\vert\varphi_i\rangle\}_{i=1}^d$ 为“两两平等基”，若

$|\langle\varphi_j\vert\psi_i\rangle|^2=\frac{1}{d}\ ,\quad \forall\ i,j$

d = 2 时，由 Bloch 球性质易证，存在三组基元，两两作成 MUB，比如取坐标轴向量

$\{\vert 0\rangle,\vert 1\rangle\},\{\vert +\rangle,\vert -\rangle\},\{\vert +i\rangle,\vert -i\rangle\}$

设 $\mathcal{H}_d$ 上这样的基元有 $\mathfrak{M}(d)$ 组，以下问题还是开问题：

是否有 $\mathfrak{M}(d)\geq 2,\ \forall\ d$
计算 $\mathfrak{M}(d)$

已有结论：

$\mathfrak{M}(N)=N+1\quad if\ N=p^r,\ where\ p\ is\ prime$

比如 $\mathfrak{M}(2)=3,\mathfrak{M}(3)=4,\mathfrak{M}(4)=5$ ，但 $\mathfrak{M}(6)$ 还未知。

参考维基：Mutually_unbiased_bases

qisikit