唠唠闲话

上学期接触了极值图问题，课余用 Mathematica（简称 MMA）算低阶结论后就没再深入。今天交接，写篇博客介绍之前用的工具。

附：低阶计算结论。

概要

本篇介绍 MMA 图论工具 IGraphM ，学过 MMA 或者对相关编程感兴趣的可以看看，附 MMA 安装教程。

参考链接
Github 项目地址：IGraphM
官方文档：A Mathematica interface for igraph

安装及演示

安装 IGraphM 函数包

  1. 进入发行页，下载 .paclet 文件
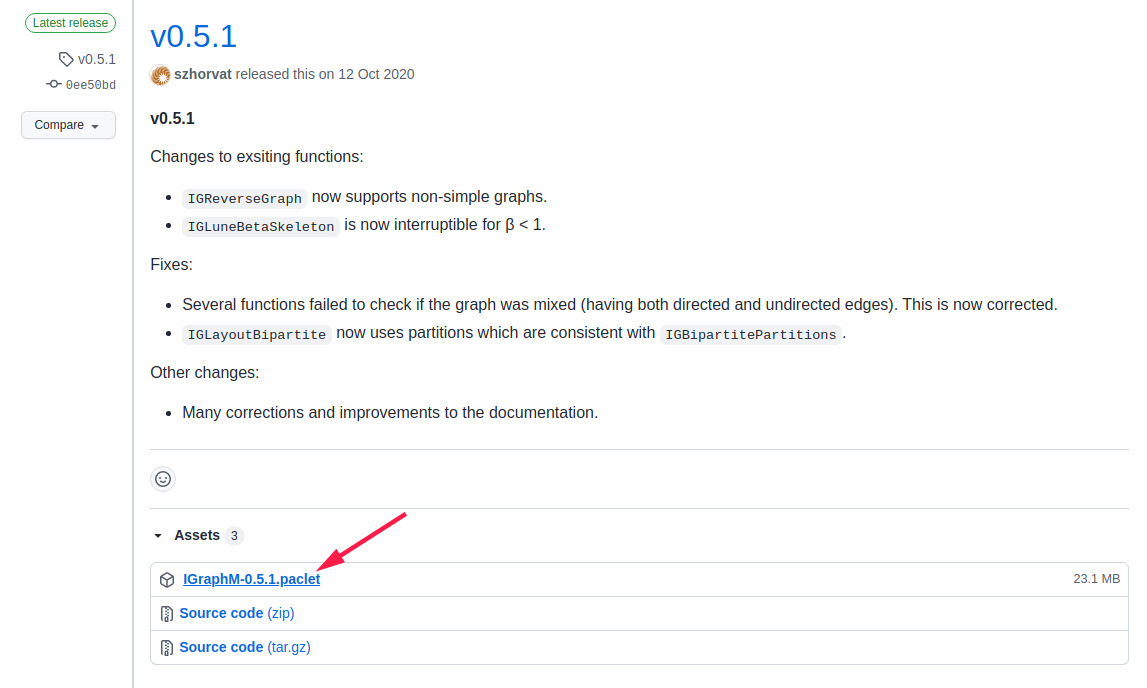
    20210924170119

  2. 打开 Mathematica ，新建笔记本
    20210924164951

  3. 执行下边命令，安装模块
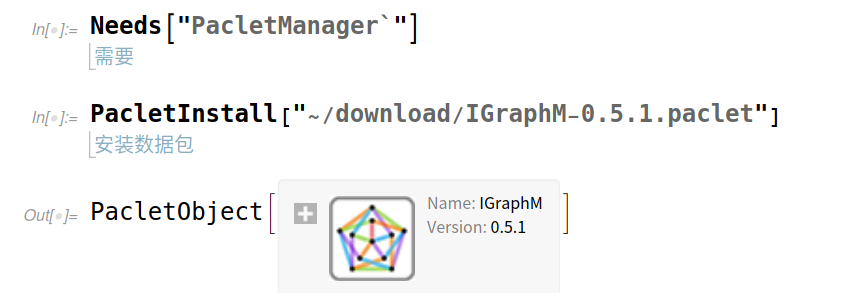
    20210924170533
    注意 ～/download/IGraphM-0.5.1.paclet 改自己文件的下载路径

下载分类数据

在 这里 下载低阶图的分类数据，建议下载前 9 阶。
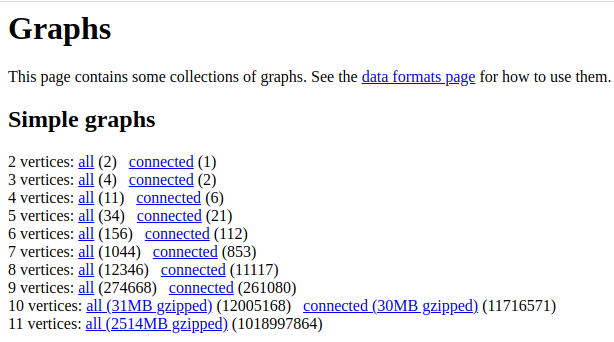
simplegraphs

自编函数

  1. 点这里下载文件 Extremal.m。
  2. 打开文件，修改 path 参数为前边简单图的下载路径
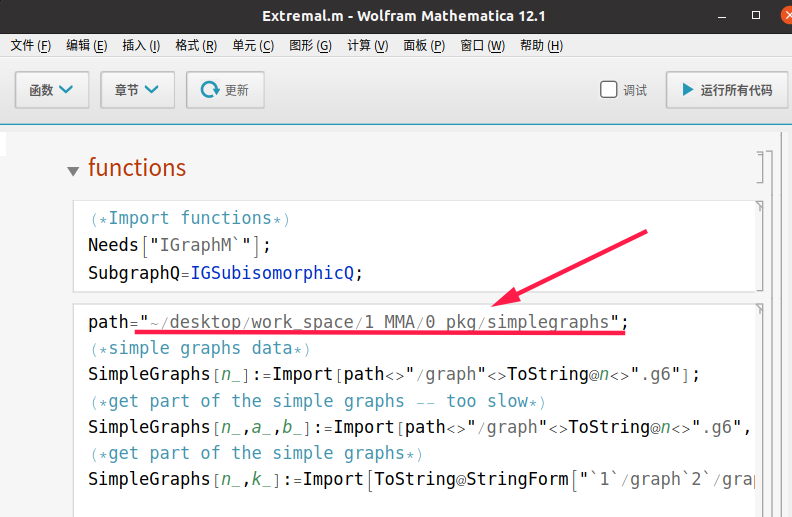
    20210924185114

使用演示

  1. 在 Extremal.m 文件所在目录，新建 notebook 文件。

  2. 导入模块
    import

  3. 求极值图和边数

    1
    2
    3
    forbidden = GraphF[1];
    graphs = SimpleGraphs[7];
    ExtremalGraphs[graphs, forbidden]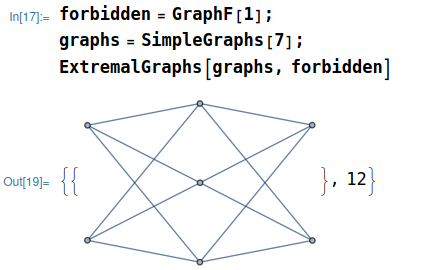

    extremal

IGraphM

下边介绍工具 IGraphM。

官方简介（谷歌直译）

IGraph/M 是用于复杂网络和图论研究的 Mathematica 包。 Mathematica 已经拥有广泛的图论和网络分析功能，而 IGraph/M 并不打算取代它。相反，它旨在补充它并与之集成，因此两个系统的功能可以无缝地一起使用。它还提供了许多核心 igraph 库中不存在的功能。因此它直接与 Mathematica 的 Graph 数据类型一起工作。

IGraphM 本身是个强大的图论工具，我只用了一个判断子图的函数，其他没去探索
20210924163721

图同构类

nauty and Traces 是用 C 语言写的工具，专门用于计算图同构类。前边下载的数据就是用 nauty 生成的。

nauty 给的这个网站上，还有其他类型图的数据（文件后缀为 .g6 本质上是文本文件，每行表示一个图）。
20210924175914

运行问题

简单图的数目随阶数指数增长。

我的电脑配置一般， CPU 是 I5 1.00GHz，遍历前 8 阶用十几秒，第 9 阶要一分多钟，第 10 阶预估要半个多小时。

这是单线程运行的情况，多线程跑第 10 阶花了 5 分多钟。（并行计算没用对，加上异步IO 会更快，待修改）

代码释义

下边解释程序代码。

定义和判断子图

  1. 导入模块 IGraphM

    1
    Needs["IGraphM`"]

  2. 定义无向图
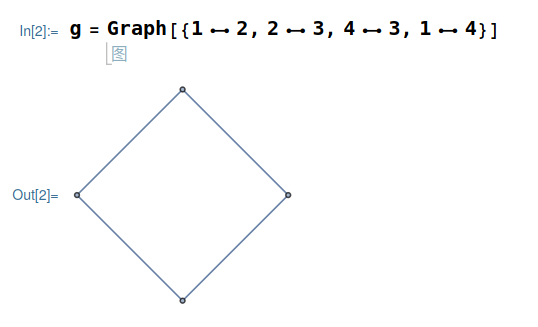
    20210924171130
    MMA 中，特殊符号用键盘左上角的 Esc 包含得到，比如无向边为 Esc ue Esc

  3. 判别是否为子图
    issubgraph

解析：

  • 第二行 CompleteGraph 是 MMA 自带的函数，返回完全图
  • 第四行 IGSubisomorphicQ 是模块 IGraphM 里的函数

自编函数

低阶简单图

编写函数 SimpleGraphs：

1
2
path= "<下载路径>/";
SimpleGraphs[n_]:= Import[path<>"/graph"<>ToString@n<>".g6"];

path 后接之前的下载路径，注意末尾加 /；输入 SimpleGraphs[n] 可以得到 n 阶简单图（n<=9）

生成子图

  1. 编写函数 GraphF 和 GraphK3

    1
    2
    3
    4
    5
    6
    7
    8
    9
    GraphF[k_?Positive]:=Module[{vertices1,vertices2,edges},
    vertices1=Range@k;
    vertices2=Range[-1,-k,-1];
    edges=(0<->#&)/@Join[vertices1,vertices2];
    edges=Join[edges,Thread[TwoWayRule[Range@k,Range[-1,-k,-1]]]];
    Graph@edges];

    (*Disjoint union of triangules*)
    GraphK3[k_?Positive]:=GraphDisjointUnion@@ConstantArray[GraphF@1,k];

  2. 使用示例
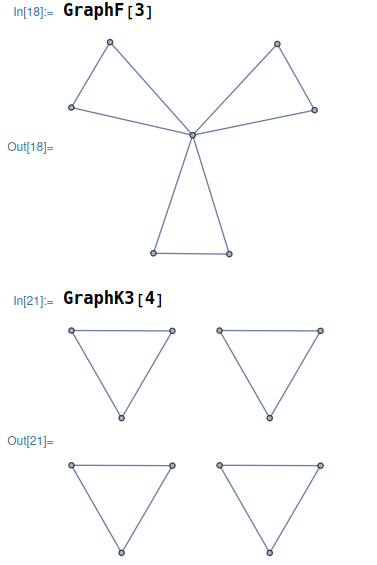
    graphf

求极值图和边数

编写函数 ExtremalGraphs

1
2
3
4
5
6
7
8
9
10
(*search for graphs in "graphs"*)

ExtremalGraphs[graphs_, forbidden_, edge_ : 0] := 
Module[{selected, maxedge},
selected = 
Select[graphs, 
    EdgeCount@# >= edge && ! IGSubisomorphicQ[forbidden, #] &];
If[Length@selected == 0, Return@{{}, edge}];
maxedge = EdgeCount /@ selected // Max;
{Select[selected, EdgeCount@# == maxedge &], maxedge}]